In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
To solve the problem, we will follow these steps:
Given:
- Parallelogram ABCD
- P is the midpoint of AB
- CP and BD intersect at point O
- Area of triangle POB = 40 cm²
- OP:OC = 1:2
Step 1: Find the area of triangle BOC
Since the ratio of OP to OC is 1:2, the area of triangle POB is also in the same ratio to the area of triangle BOC.
Let:
- Area of triangle POB = 40 cm²
- Area of triangle BOC = x cm²
From the ratio, we have:
Area of POBArea of BOC=12
Substituting the known area:
40x=12
Cross-multiplying gives:
40⋅2=1⋅x⟹x=80 cm²
Step 2: Find the area of triangle PBC
The area of triangle PBC can be found by adding the areas of triangles POB and BOC:
Area of PBC=Area of POB+Area of BOC=40 cm²+80 cm²=120 cm²
Step 3: Find the area of triangle ABC
Since CP is the median of triangle ABC, it divides triangle ABC into two equal areas. Therefore, the area of triangle ABC is twice the area of triangle PBC:
Area of ABC=2×Area of PBC=2×120 cm²=240 cm²
Step 4: Find the area of parallelogram ABCD
The diagonal AC divides the parallelogram ABCD into two equal triangles (ABC and ADC). Therefore, the area of parallelogram ABCD is twice the area of triangle ABC:
Area of parallelogram ABCD=2×Area of ABC=2×240 cm²=480 cm²
Final Answers:
(i) Area of triangle BOC = 80 cm²
Area of triangle PBC = 120 cm²
(ii) Area of triangle ABC = 240 cm²
Area of parallelogram ABCD = 480 cm²
---
- Parallelogram ABCD
- P is the midpoint of AB
- CP and BD intersect at point O
- Area of triangle POB = 40 cm²
- OP:OC = 1:2
Since the ratio of OP to OC is 1:2, the area of triangle POB is also in the same ratio to the area of triangle BOC.
- Area of triangle POB = 40 cm²
- Area of triangle BOC = x cm²
Area of POBArea of BOC=12
Substituting the known area:
40x=12
Cross-multiplying gives:
40⋅2=1⋅x⟹x=80 cm²
The area of triangle PBC can be found by adding the areas of triangles POB and BOC:
Area of PBC=Area of POB+Area of BOC=40 cm²+80 cm²=120 cm²
Since CP is the median of triangle ABC, it divides triangle ABC into two equal areas. Therefore, the area of triangle ABC is twice the area of triangle PBC:
Area of ABC=2×Area of PBC=2×120 cm²=240 cm²
The diagonal AC divides the parallelogram ABCD into two equal triangles (ABC and ADC). Therefore, the area of parallelogram ABCD is twice the area of triangle ABC:
Area of parallelogram ABCD=2×Area of ABC=2×240 cm²=480 cm²
(i) Area of triangle BOC = 80 cm²
Area of triangle PBC = 120 cm²
Area of parallelogram ABCD = 480 cm²
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
Knowledge Check

The given figure shows a parallelogram ABCD whose diagonals intersect each other at point O. if OB=6 cm and AC is 6 cm more than BD, find OC.A12cmB10cmC9cmD11cm
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF:FE= 5:3 and area of ΔADF is 60cm2, find :
(i) area of ΔADE
(ii) if AE:EB= 4:5, find the area of ΔADB
(iii) also, find area of parallelogram ABCD.
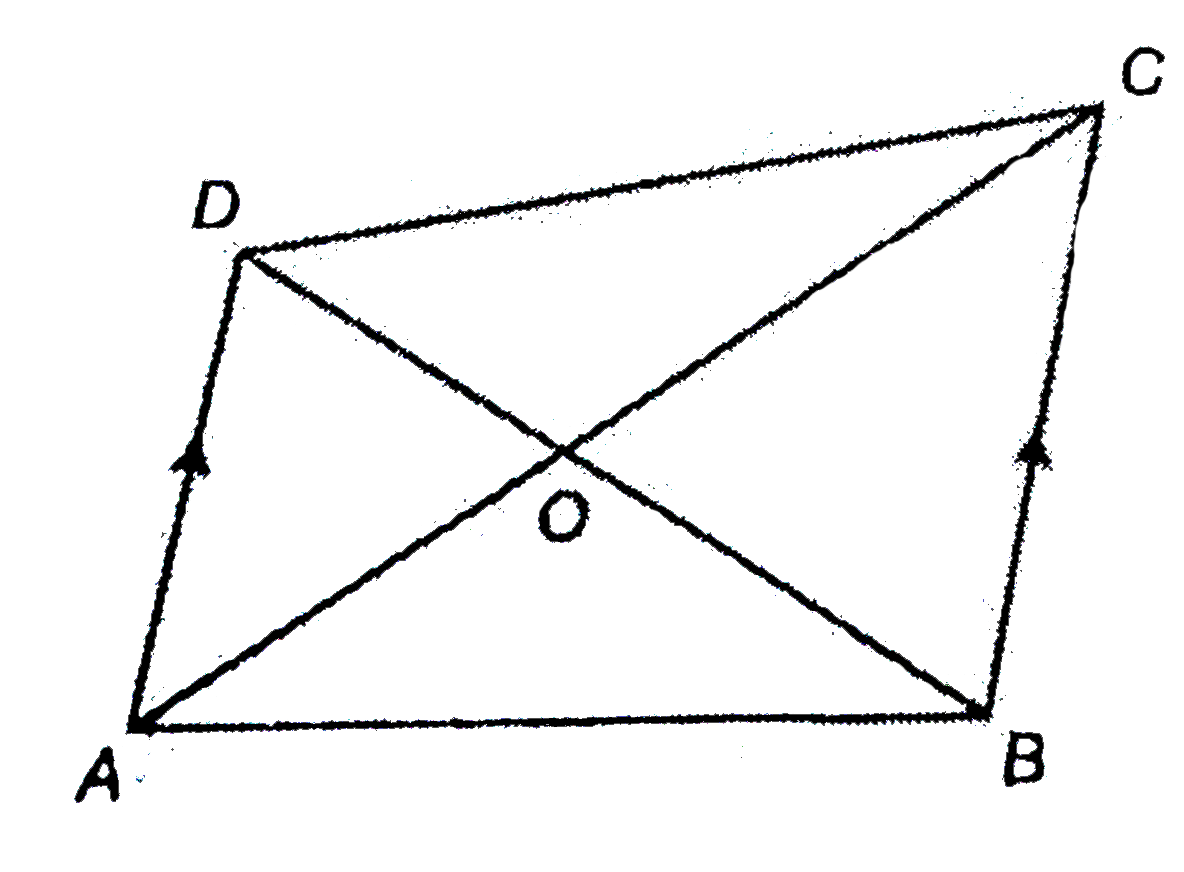
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
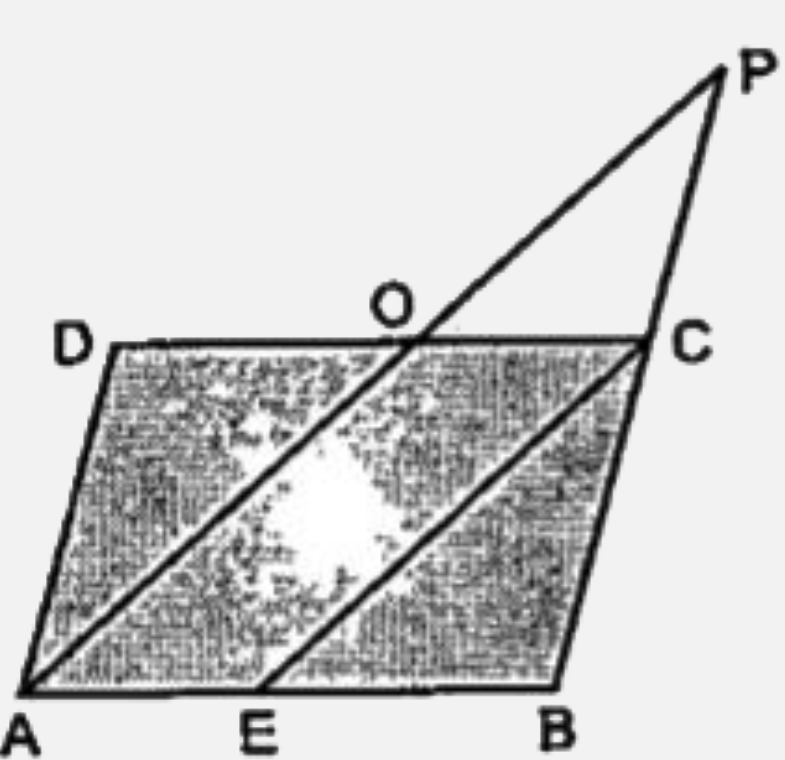
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
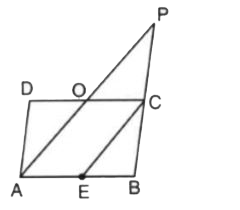
PB=2AD
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View SolutionThe diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the ratio of the areas of triangle AOB and COD.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View Solution
