In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
Step by step video & image solution for In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of DeltaPOB=40cm^(2) and OP:OC= 1:2, find : (i) Areas of DeltaBOC and DeltaPBC (ii) Areas of DeltaABC and parallelogram ABCD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
Knowledge Check

The given figure shows a parallelogram ABCD whose diagonals intersect each other at point O. if OB=6 cm and AC is 6 cm more than BD, find OC.A12cmB10cmC9cmD11cm
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF:FE= 5:3 and area of ΔADF is 60cm2, find :
(i) area of ΔADE
(ii) if AE:EB= 4:5, find the area of ΔADB
(iii) also, find area of parallelogram ABCD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
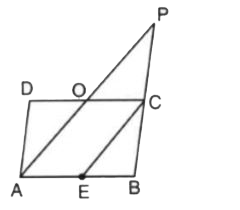
PB=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
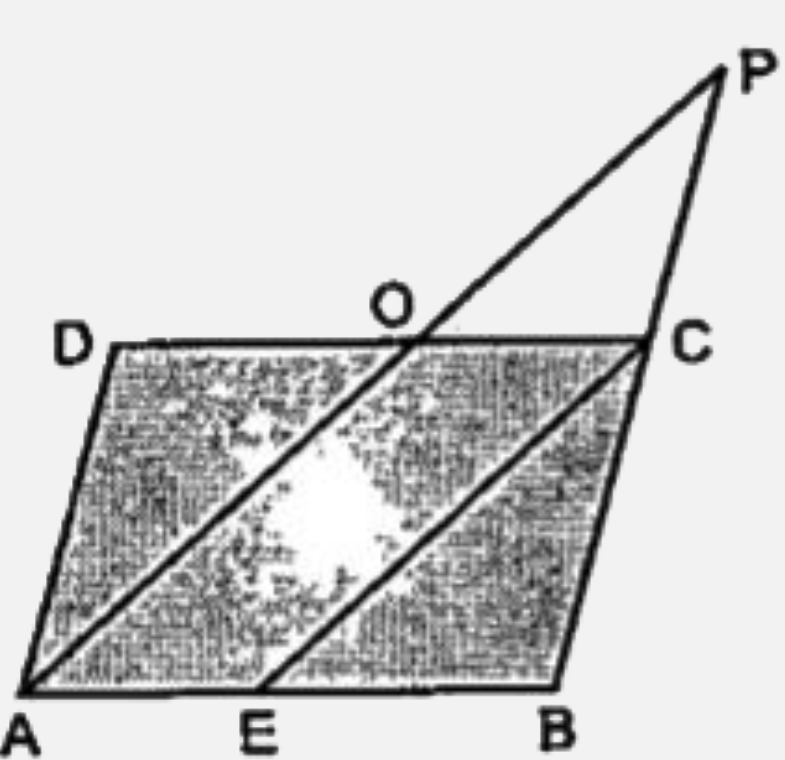
BP=2AD
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View SolutionThe diagonals of a trapezium ABCD with AB||DC intersect each other at point O. If AB = 2CD, find the ratio of the areas of triangle AOB and COD.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View Solution
