In the 20 th row of the triangle

A

$6 / 5$

B

$7 / 2$

C

$9 / 5$

D

none of these

Text Solution

Verified by Experts

The correct Answer is:B

Let the first term be a and common difference be d for the first A.P. and the first term be b and common difference be e for the second A.P. and let the numbers of terms be n. Then
$\frac{a + (n - 1) d}{b} = \frac{b + (n - 1) e}{a} = 4$ (1)
$\frac{\frac{n}{2} [2 a + (n - 1) d]}{\frac{n}{2} [2 b + (n - 1) e]} = 2$ (2)
From (1) and (2), we get
a-4b+(n-1)d=0 (3)
b-4a+(n-1)e=0 (4)
2a-4b+(n-1)d-2(n-1)e=0 (5)
$4 \times (3) + (4)$ gives
$- 15 b + 4 (n - 1) d + (n - 1) e = 0$ (6)
$(4) + 2 \times (5)$ gives
$- 7 b + 2 (n - 1) d - 3 (n - 1) e = 0$ (7)
Further, $15 \times (7) - 7 \times (6)$ gives
$2 (n - 1) d - 52 (n - 1) e = 0$
or d=26e $(∵ n > 1)$
$∴ d / e = 26$
Putting d=26e in (3) and solving it with (4), we get
a=2(n-1)e,b=7(n-1)e
Then, the ratio of their $n^{t h}$ terms is
$\frac{2 (n - 1) + (n - 1) 26 e}{7 (n - 1) e + (n - 1) e} = \frac{7}{2}$

|

Class 12 MATHS PROGRESSION AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Sum of all the terms in the nth row of the triangle
is
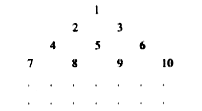A $\frac{1}{2} n^{2} (n + 1)$
B $\frac{1}{2} n (n^{2} + 1)$
C $n (n^{2} + 1)$
D $n^{2} (n + 1)$
The sum of the elements in the sixth row of Pascal triangle is ___________
A32
B63
C128
D64
If Ravindra finds that he is $20^{t h}$ from the right end in a row of boys and $6^{t h}$ from the left end, how many boys should be added to the row such that there are 36 boys in the row?
A12
B11
CCannot be determined
D13

CENGAGE PUBLICATION-PROGRESSION AND SERIES-EXERCIESE ( LINKED COMPREHENSION TYPE )

Home
Ask Doubt
Profile