In the adjacent figure a parabola is drawn to pass through the vertices B,C and D of the square ABCD. If A(2,1),C(2,3), then focus of this parabola is

(1,114)
(2,114)
(3,134)
(2,134)
The correct Answer is:B
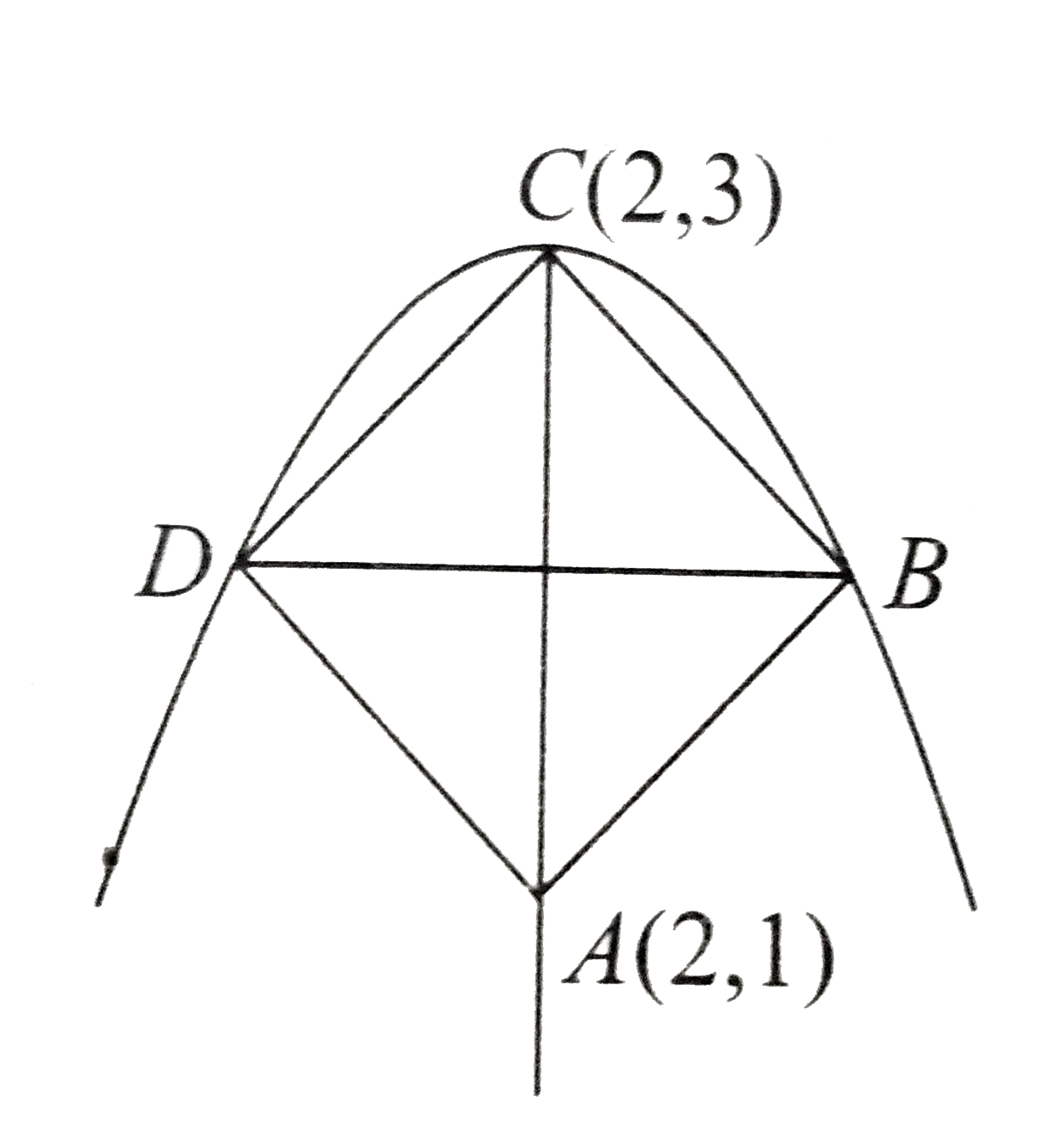
AC is parallel to y-axis and its mid-point is (2,2). Thus, B≡(3,2) and D≡(1,2).
Equation of parabola,
(x−2)2=λ(y−3)
It passes through (3,2), so
1=−λ⇒λ=−1
∴(x−2)2=−(y−3)
Hence, axis is x−2=0,L.R. line is y−3=−14
∴ Focus ≡(2,114)
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - MULTIPLE CORRECT ANSWER TYPE
7 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
A square has one vertex at the vertex of the parabola y2=4ax and the diagonal through the vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of the vertices of the square are (a)(4a,4a) (b) (4a,−4a) (c)(0,0) (d) (8a,0)
View SolutionA parabola is drawn with focus at (3,4) and vertex at the focus of the parabola y2−12x−4y+4=0. The equation of the parabola is
View SolutionA parabola is drawn with focus at (3,4) and vertex at the focus of the parabola y2−12x−4y+4=0. The equation of the parabola is
View SolutionIf the parabola y2=ax passes through (1, 2) then the equation of the directrix is
View SolutionA parabola passes through the point the point (1,2), (2,1), (3,4) and (4,3). Find the equation of the axis of parabola.
View SolutionIn figure, arcs have been drawn of radius 21 cm each with vertices A,B,C and D of quadrilateral ABCD as centres . Find the area of the shaded region.

View SolutionIf the parabola y2=4ax passes through the point (4, 1), then the distance of its focus the vertex of the parabola is
View SolutionA parabola y=ax2+bx+c with a>0 passes through the points (-2,3)(pq), and (5,3). If (p,q) is the lowest point on the parabola, what is the value of p?
View SolutionP(2,2),Q(−2,2)R(−2,−2)&S(2,−2) are vertices of a square. A parabola passes through P.S& its vertex liesn on x-axis. If this parabola bisect the area of the square PQRS, then vertex of the parabola
View SolutionThe line x+y+2=0 is a tangent to a parabola at point A, intersect the directrix at B and tangent at vertex at C respectively. The focus of parabola is S(a,0). Then
View Solution
