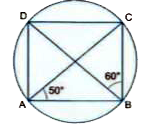
In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠DBC=60∘ and ∠BAC=40∘ , then find the value of ∠BCD .
Video Solution
Text Solution
Since, ABCD is a cyclic quadrilateral .
∴∠DAC=∠DBC=60∘
and ∠DAB=∠DAC+∠CAB
=60∘+40∘
=100∘
Now, ∠DAB+∠BCD=180∘
⇒100∘+∠BCD=180∘
∠BCD=180∘−100∘
=806∘ .
|
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
In the adjoining figure, ABCD is a cyclic quadrilateral . If ∠CBX=104∘ and ∠CAB=56∘, then find the value of ∠ADB.
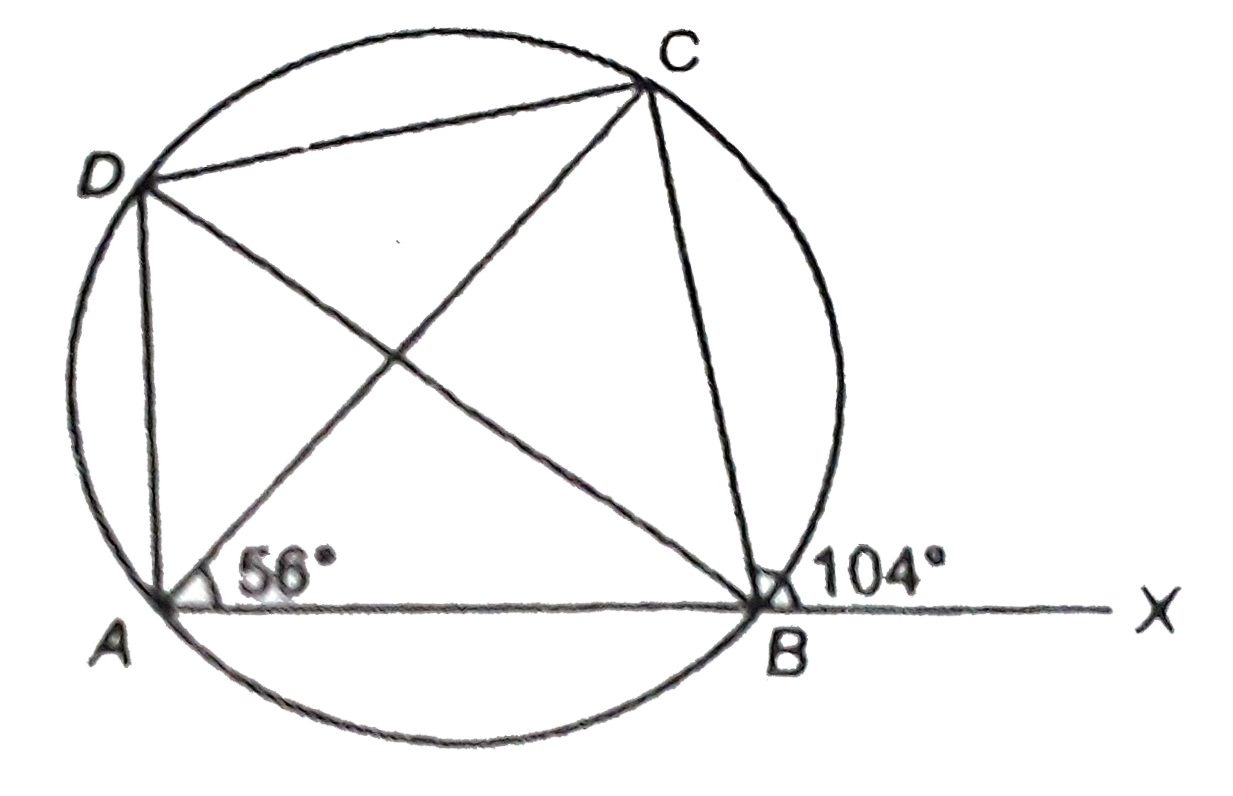 A28∘B48∘C58∘D18∘
A28∘B48∘C58∘D18∘In the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
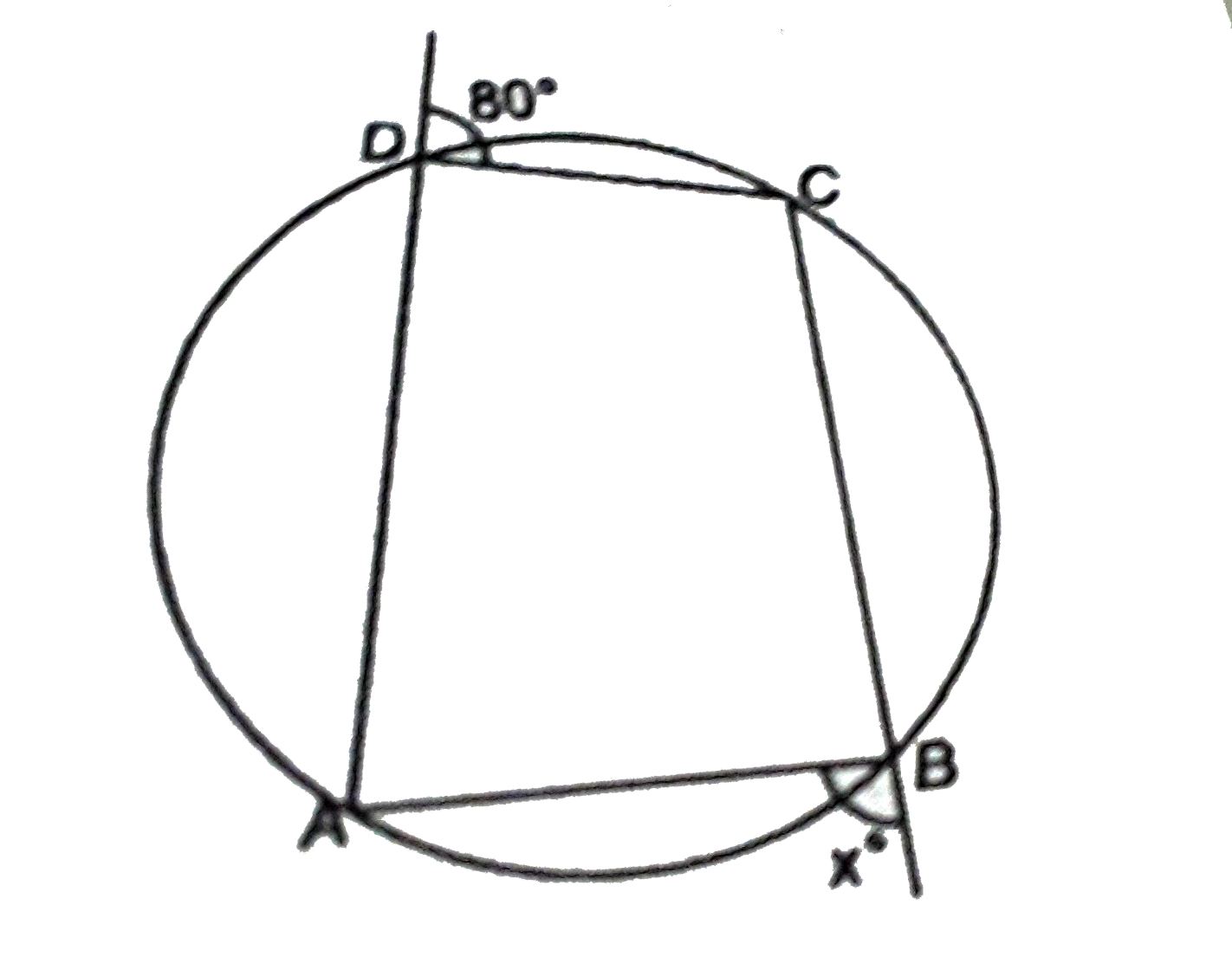 A60∘B80∘C100∘D120∘
A60∘B80∘C100∘D120∘In the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :
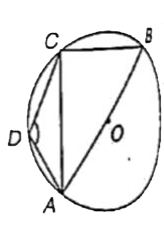 A45∘B40∘C50∘Dnone of the above
A45∘B40∘C50∘Dnone of the above
In the given diagram ABCD is a cyclic quadrilateral ∠OCB=50∘ and ∠BOC=110∘ Find the value of ∠DAO :
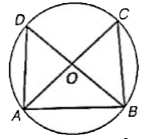
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
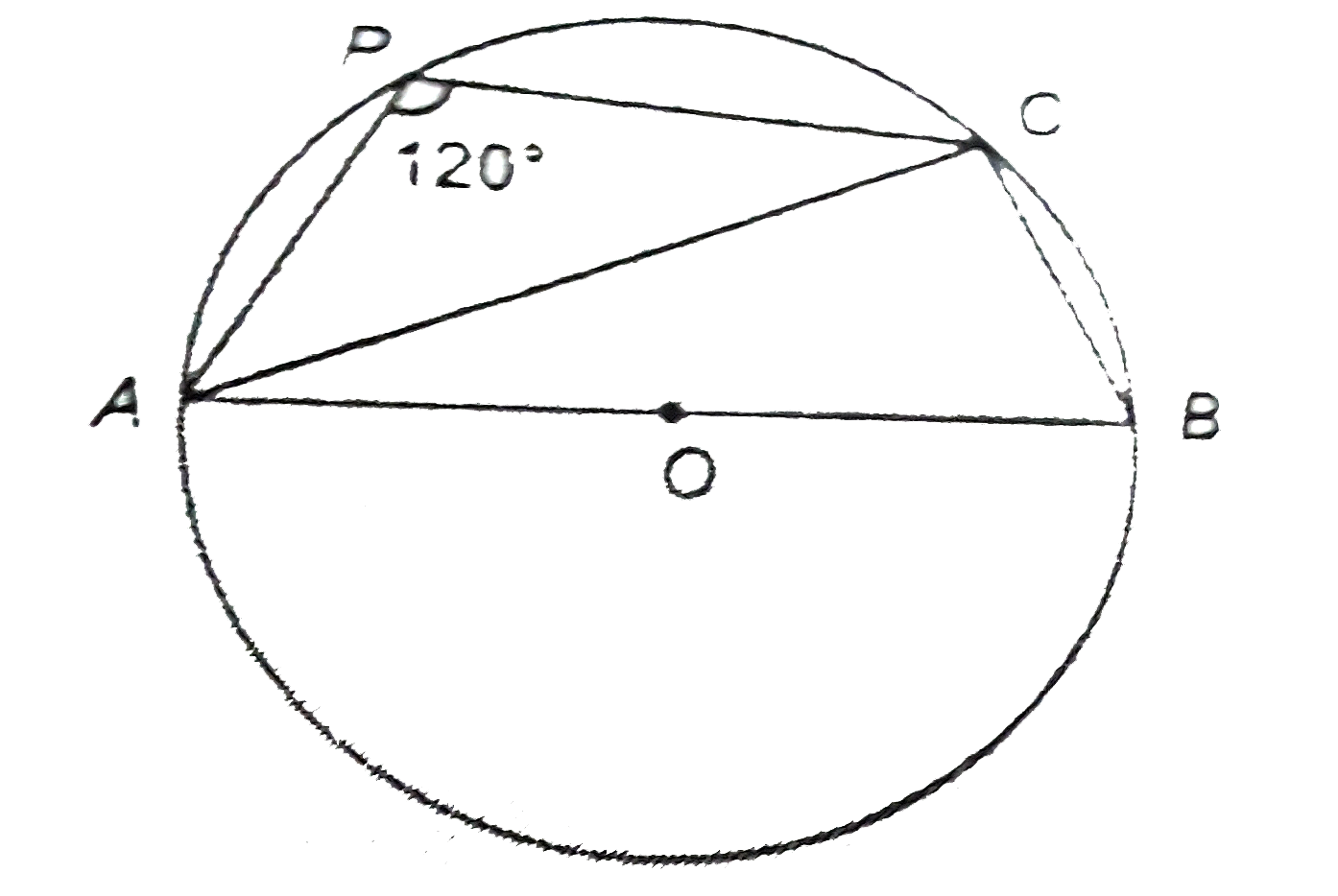
View Solution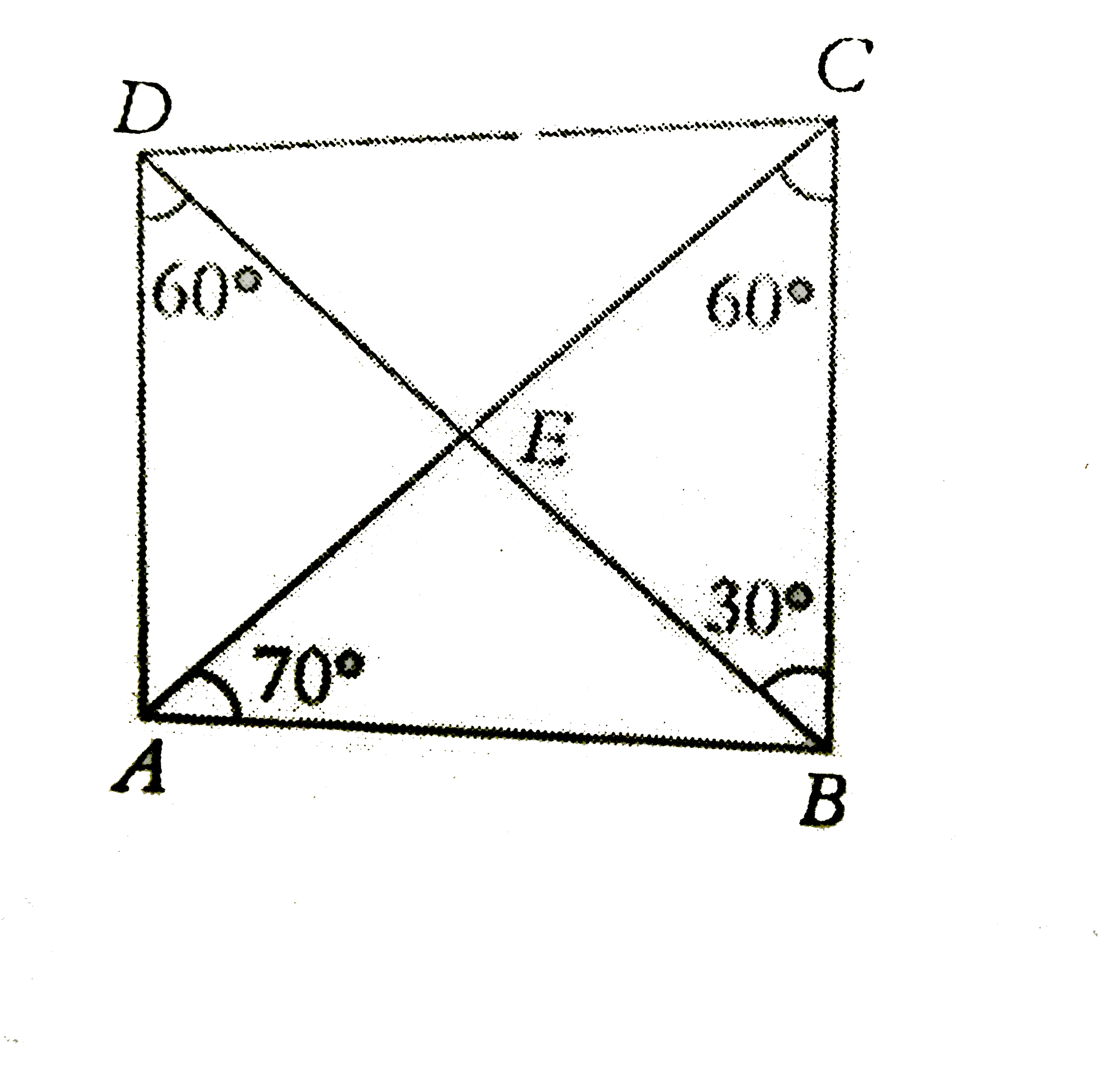
In the given figure, ABCD is a quadrilateral ∠ADB=60∘,∠BAC=70∘,∠DBC=30∘, and
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of x
View SolutionIn the adjoining figure, the area of quadrilateral ABCD is
View Solution