In the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of . Prove that:
(i) is a parallelogram
(ii) area of
(iii) area of
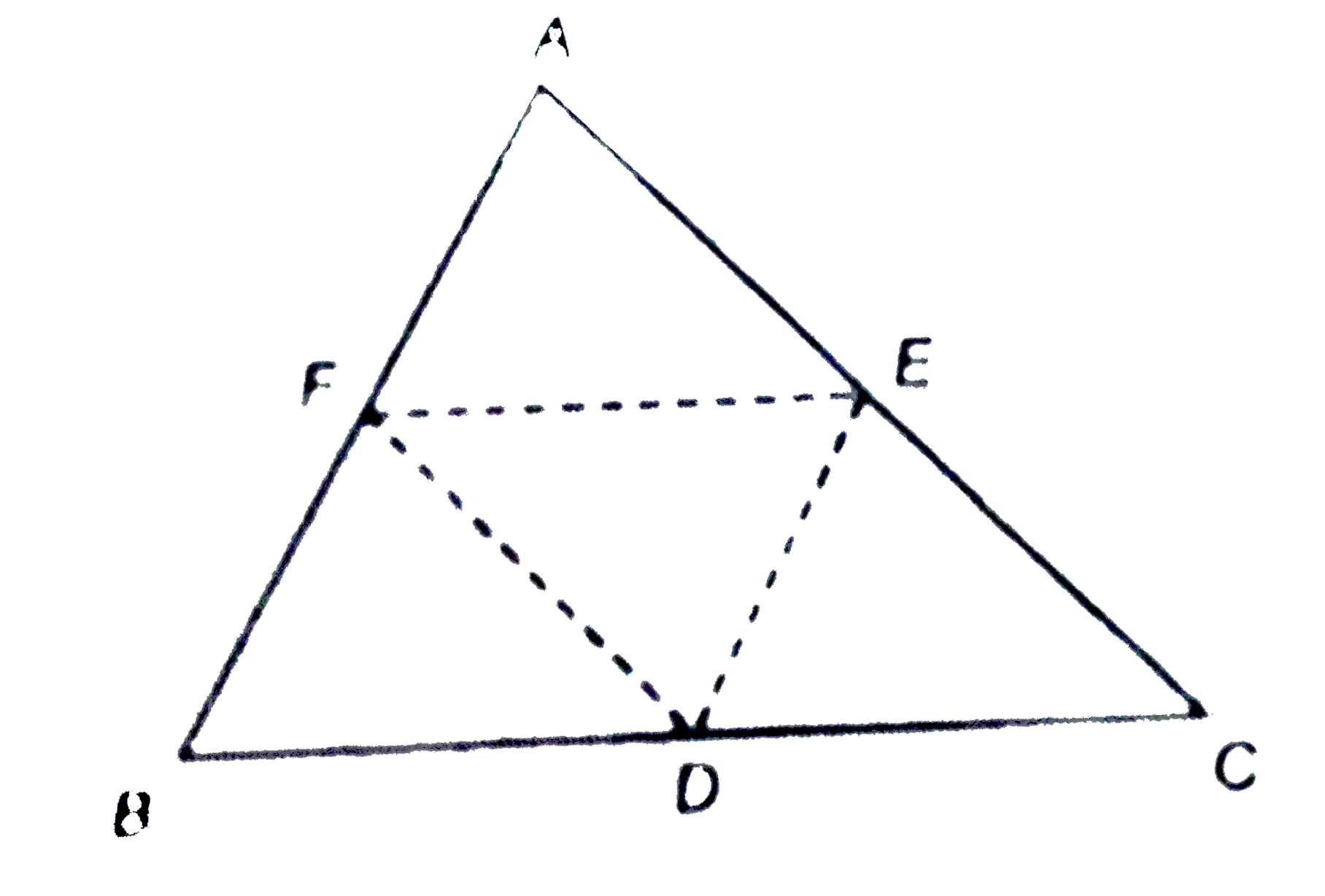
(i) In
Since, F is the mid-point of AB and E is the mid-point of AC
(mid - point theorem)
is a parallelogram ( pairs of opposite sides are parallel)
(ii) Since, is a parallelogram and FD is its diagonal
area of ..(1)
Similarly, we can prove that
area of ...(2)
and area of ...(3)
= area of
(iii) Now, area of
( diagonal divides the parallelogram into two equal areas)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise34videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF - Question 2 - Select One
In a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF - Question 3 - Select One
If D, E and F are the mid points of BC, CA and AB respectively of the △ABC then the ratio of aria parallelogram DEFB and area of the trapezium CAFD is ,
A2:3B3:4C1:2D1:3
D, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
 View Solution
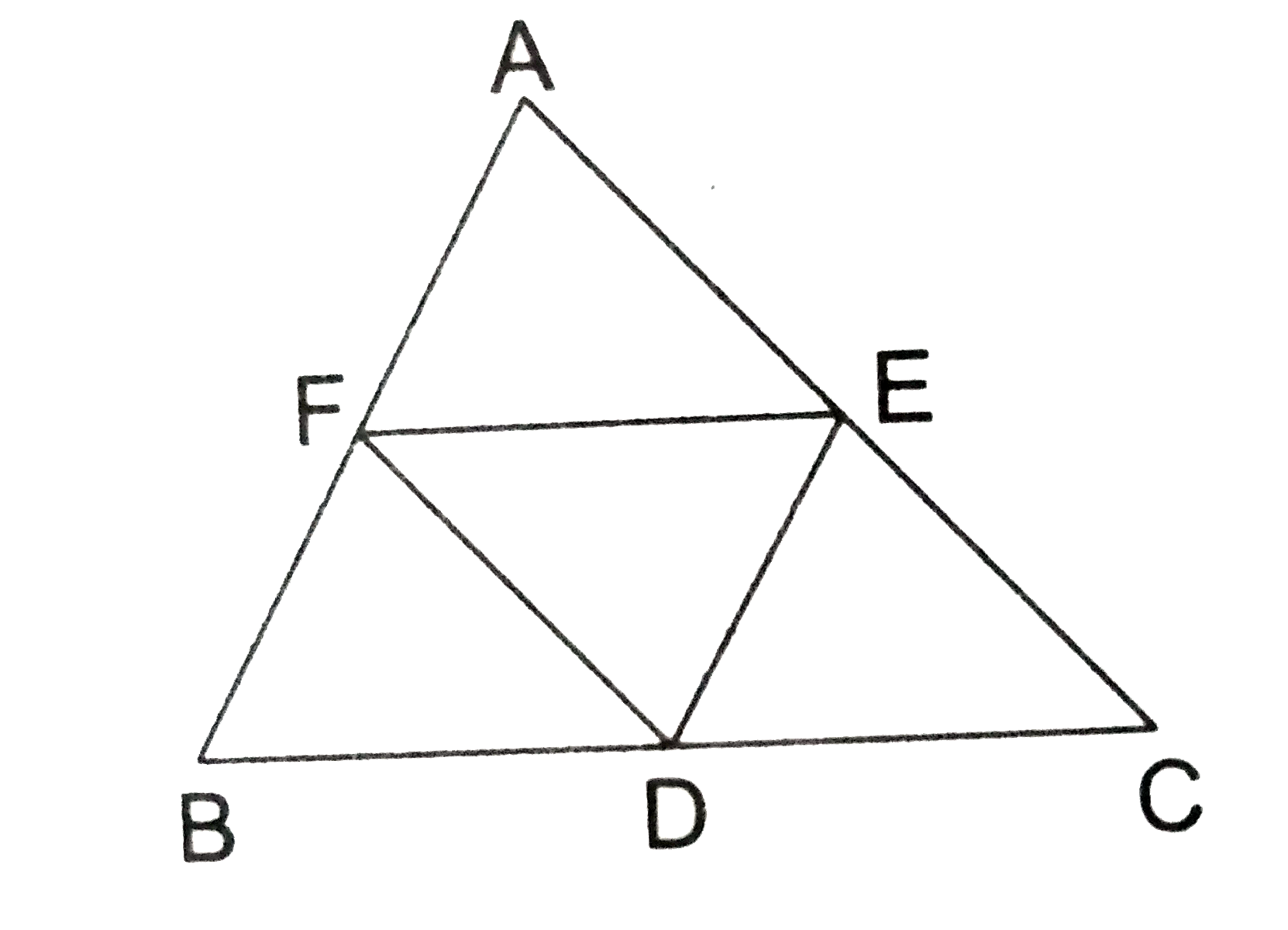
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
 View Solution
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View Solution


