In the adjoining figure, find the area of the shaded region (Use π=3.14)
To find the area of the shaded region in the given figure, we will follow these steps:
Step 1: Identify the dimensions of the rectangle
The rectangle has a length of 8 cm and a breadth of 6 cm.
Step 2: Calculate the area of the rectangle
The area of a rectangle is given by the formula:
Area of Rectangle=Length×Breadth
Substituting the values:
Area of Rectangle=8cm×6cm=48cm2
Step 3: Determine the diameter of the circle
The diagonal of the rectangle serves as the diameter of the circle. We can find the length of the diagonal using the Pythagorean theorem:
Diagonal2=Length2+Breadth2
Substituting the values:
Diagonal2=82+62=64+36=100
Taking the square root:
Diagonal=√100=10cm
Step 4: Calculate the radius of the circle
The radius R of the circle is half of the diameter:
R=Diameter2=10cm2=5cm
Step 5: Calculate the area of the circle
The area of a circle is given by the formula:
Area of Circle=πR2
Using π=3.14:
Area of Circle=3.14×(5cm)2=3.14×25cm2=78.5cm2
Step 6: Calculate the area of the shaded region
The area of the shaded region is found by subtracting the area of the rectangle from the area of the circle:
Area of Shaded Region=Area of Circle−Area of Rectangle
Substituting the values:
Area of Shaded Region=78.5cm2−48cm2=30.5cm2
Final Answer
The area of the shaded region is 30.5cm2.
---
The rectangle has a length of 8 cm and a breadth of 6 cm.
The area of a rectangle is given by the formula:
Area of Rectangle=Length×Breadth
Substituting the values:
Area of Rectangle=8cm×6cm=48cm2
The diagonal of the rectangle serves as the diameter of the circle. We can find the length of the diagonal using the Pythagorean theorem:
Diagonal2=Length2+Breadth2
Substituting the values:
Diagonal2=82+62=64+36=100
Taking the square root:
Diagonal=√100=10cm
The radius R of the circle is half of the diameter:
R=Diameter2=10cm2=5cm
The area of a circle is given by the formula:
Area of Circle=πR2
Using π=3.14:
Area of Circle=3.14×(5cm)2=3.14×25cm2=78.5cm2
The area of the shaded region is found by subtracting the area of the rectangle from the area of the circle:
Area of Shaded Region=Area of Circle−Area of Rectangle
Substituting the values:
Area of Shaded Region=78.5cm2−48cm2=30.5cm2
The area of the shaded region is 30.5cm2.
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Problems From NCERT /exemplar
25 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
In figure , find the area of the shaded region
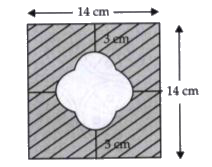
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View SolutionFind the area of the shaded region in
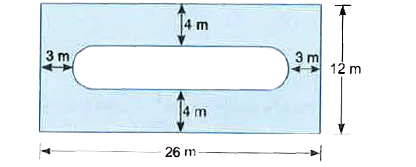
View SolutionFind the area of the shaded regions.

View SolutionIn the following figures, find the area of the shaded region.
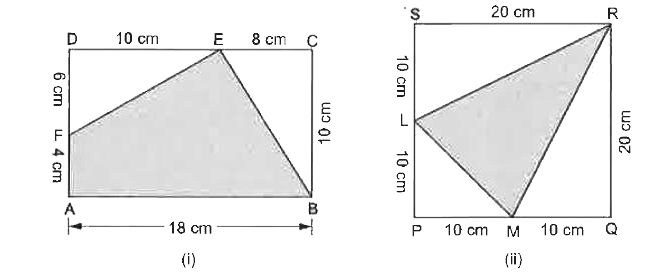
View SolutionFind the area of shaded region

View SolutionFind the area of shaded region
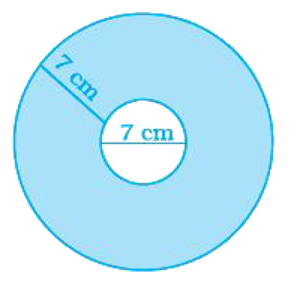
View SolutionFind the area of shaded region
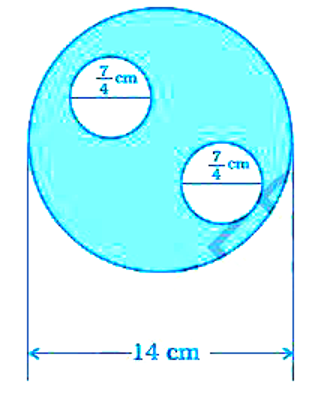
View SolutionIn figure, find the area of the shaded region. (Useπ=227)
View SolutionFind the area of shaded region.
View Solution
