In the adjoining figure, O is the centre of circle. If ∠BCD=28∘,∠AEC=38∘, then the value of ∠AXB is- Solution in Bengali
56∘
94∘
38∘
28∘
The correct Answer is:B
In the circle with centre at O, the angles ∠BADand∠BCD are both angles in circle produced by the are ⌢BD.
∴∠BAD=∠BCD=28∘ (Given )[ by theorem-35]
Again ∠AEC=38∘,∴ADC=∠AEC+∠DAB)
[∴ external ∠ADC = internally opposite (∠AEC+∠DAE]
∴∠ADC=38∘+∠BAD[∴∠DABand∠BAD are same angles]
=38∘+28∘=66∘
Again∠AXB= internally opposite (∠XDC+∠XCD)
=∠ADC+∠BCD=66∘+28∘=94∘
Hence (b) is correct.

Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False
2 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Fill in the blanks)
9 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
The number of angles in a circle produced by an fixed arc is infinte.
View SolutionOn the same circular arc, the angle in circle is __________ of its central angle.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionIn two congruent circles with centres O and O', if arc AXB subtends an angle of 75^(@) at the centre O and arcA'YB' subtends an angle of 25^(@) at the center O, Then find the ratio of arcs AXB and A'YB'
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

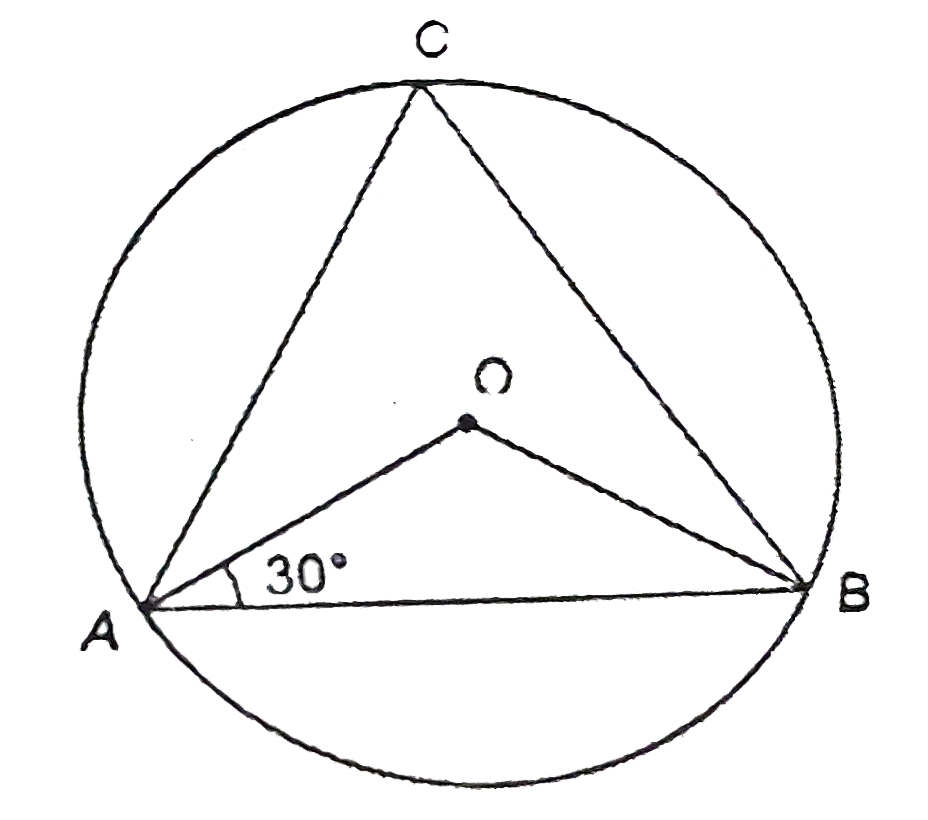
View SolutionIn the adjoining , O is the centre of the circle. ACB is a segment. If ∠OAB=30∘, then find the value of ∠ACB.
View SolutionIn the adjoining figure, AOB is the diameter and O is the centre of the circle. If ∠BDC=60∘, then find the value of ∠ABC.

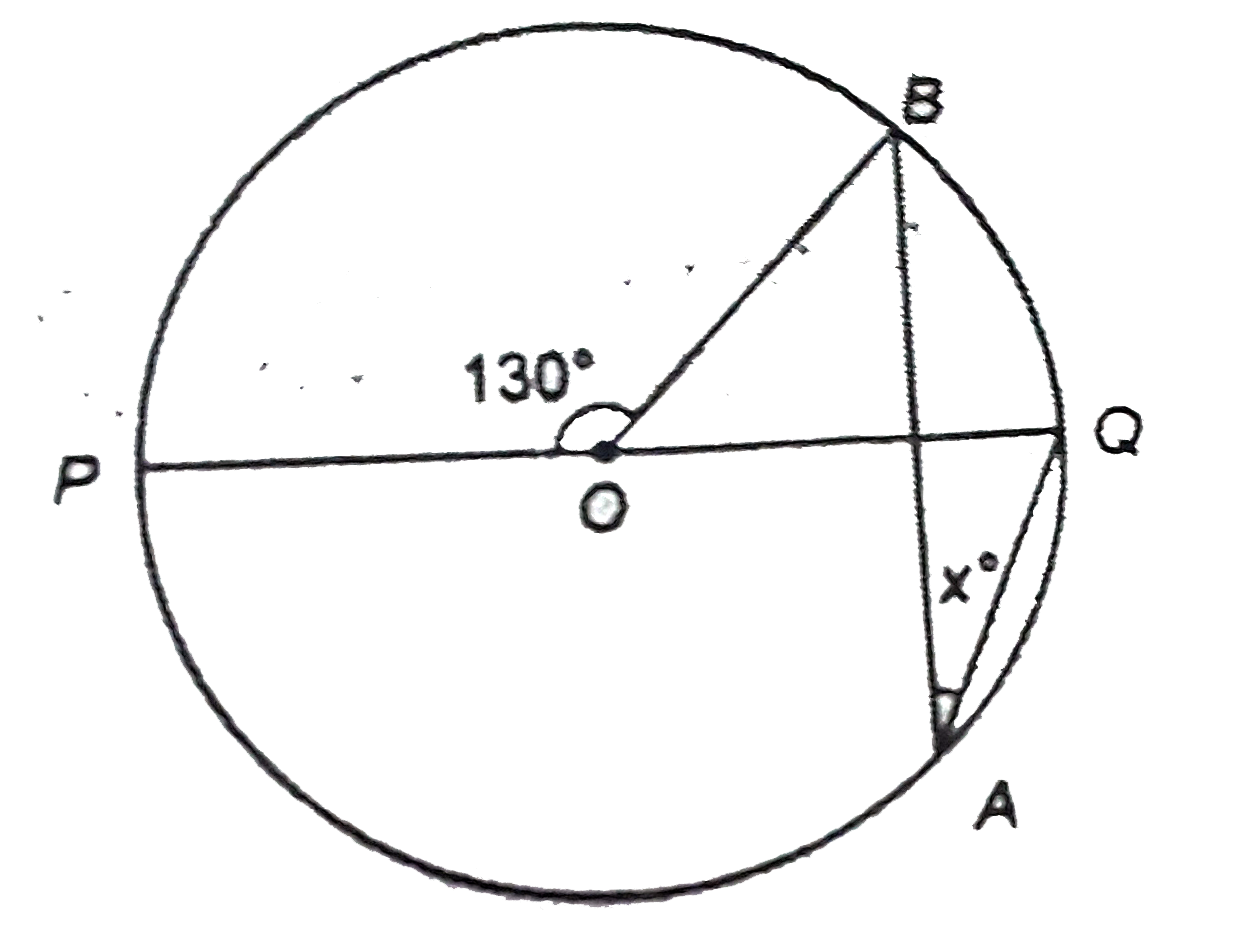
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠BOP=130∘, then find the value of x.
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=70∘, then find the value of ∠OCD.

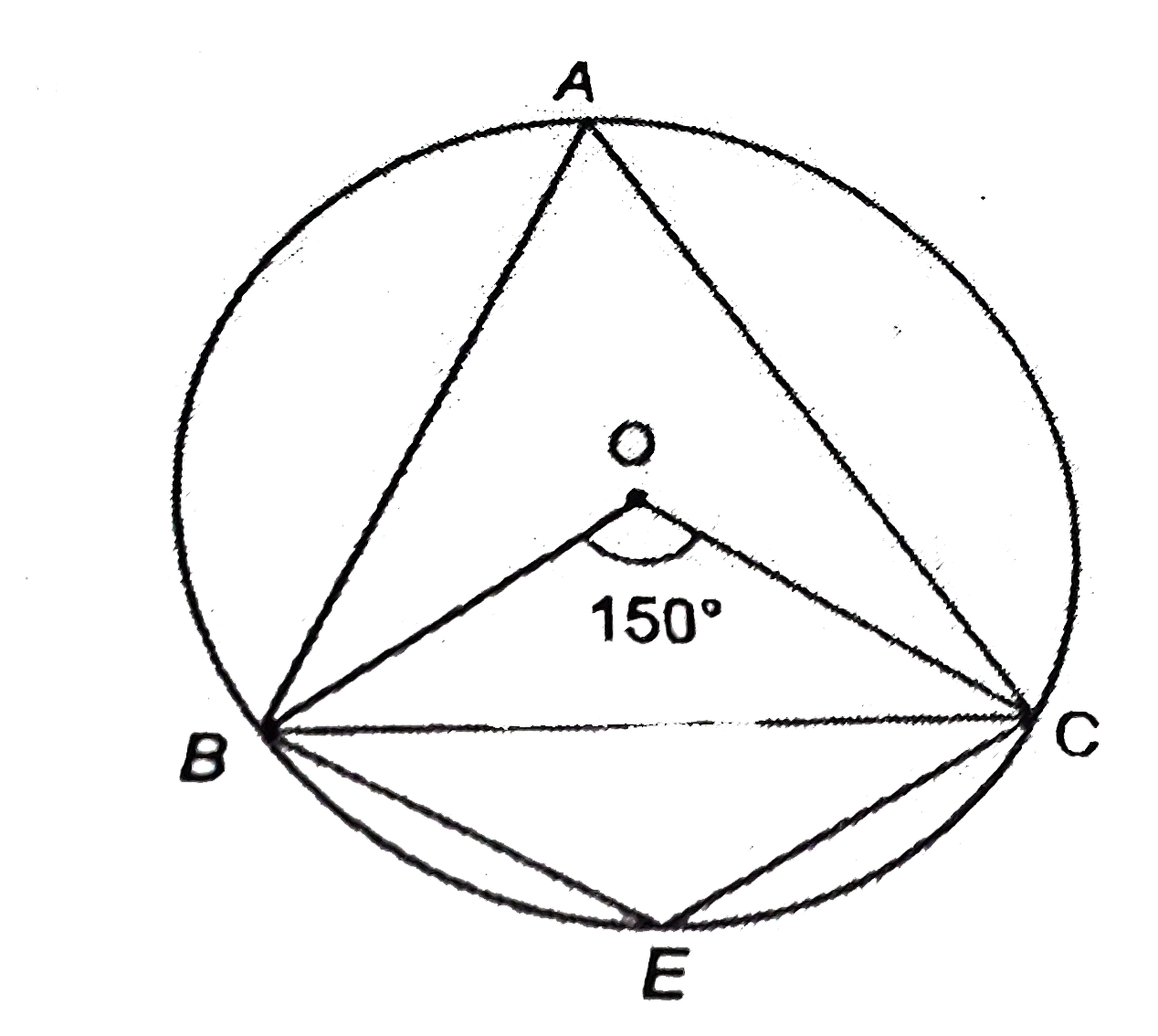
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
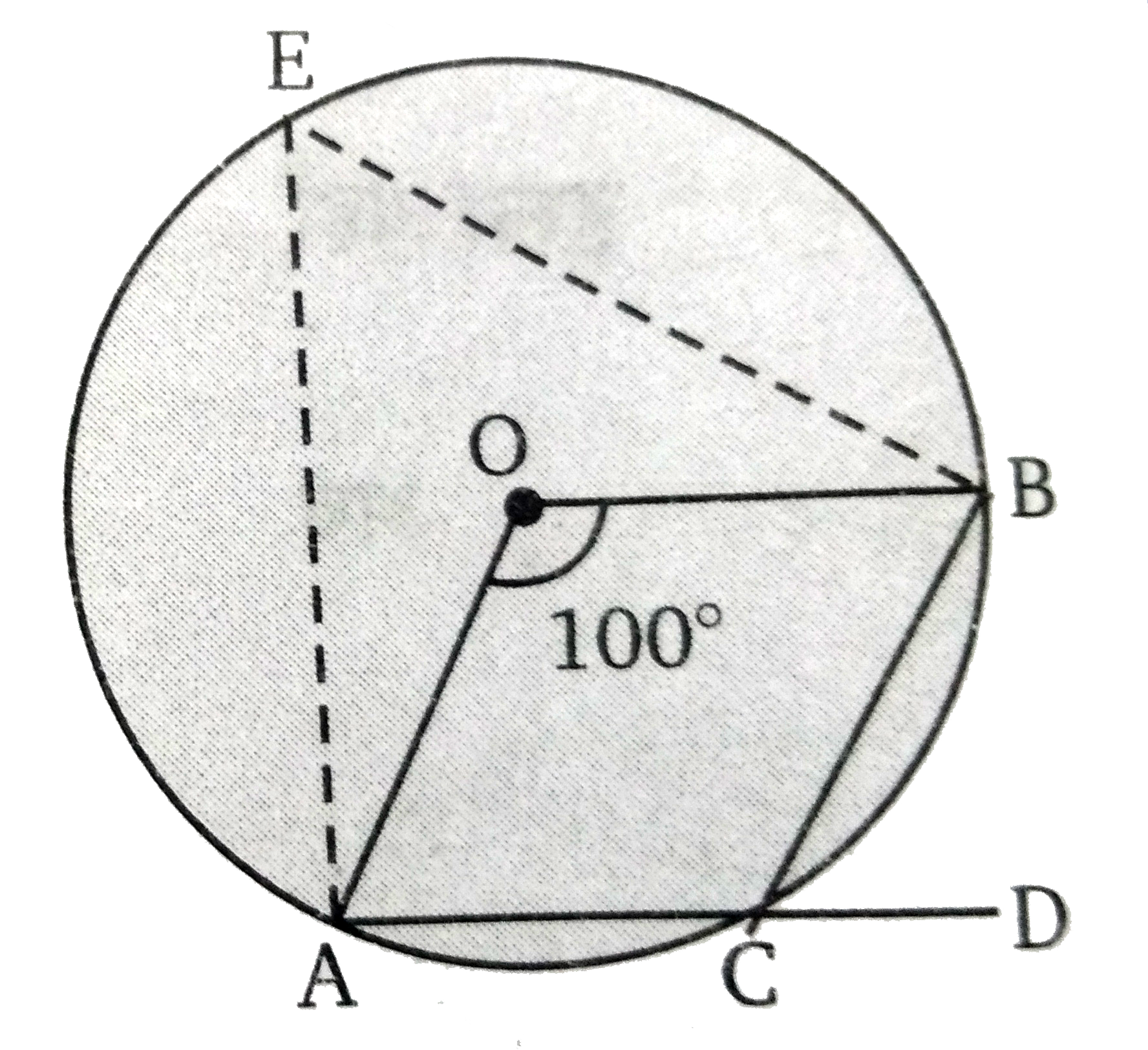
View Solutionचित्र में O , वृत्त का केन्द्र है यदि ∠AOB=100∘ तब ∠BCD का मान ज्ञात कीजिए।
View SolutionIn the adjoining figure,O is centre of the circle , If ∠ACB=30∘,∠ABC=60∘,∠DAB=35∘and∠DBC=x∘, then the value of x is
View SolutionIn the adjoining firgure, O is the centre of the circle, if ∠BAD=65∘,∠BDC=45∘ then the value of ∠CBD is
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AEB=110∘,∠CBE=30∘, then the value of ∠ADB is
View Solution
