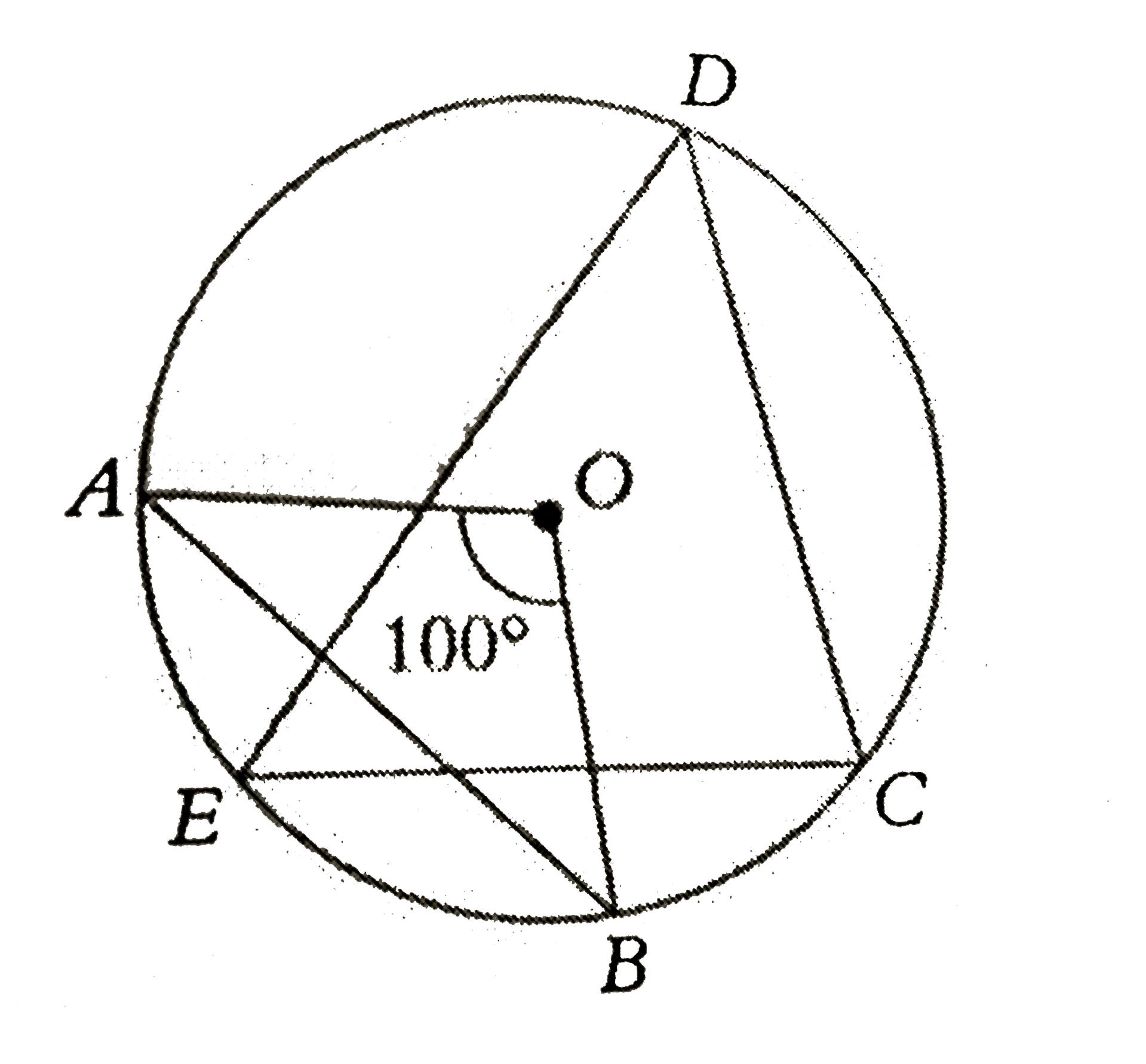In the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
Video Solution
Text Solution
Radius of circle =diameter2
⇒AO=262=13cm
AM=AB2=102=5cm,(∵perpendicular drawn from centre to the chrod bisects the chord)
Now, in ΔAOM,
AM2+OM2=AO2
⇒OM2=AO2−AM2=132−52=169−25=144
⇒OM=√144=12cm
Therefore, the distance of chord from the centre =12 cm
|
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
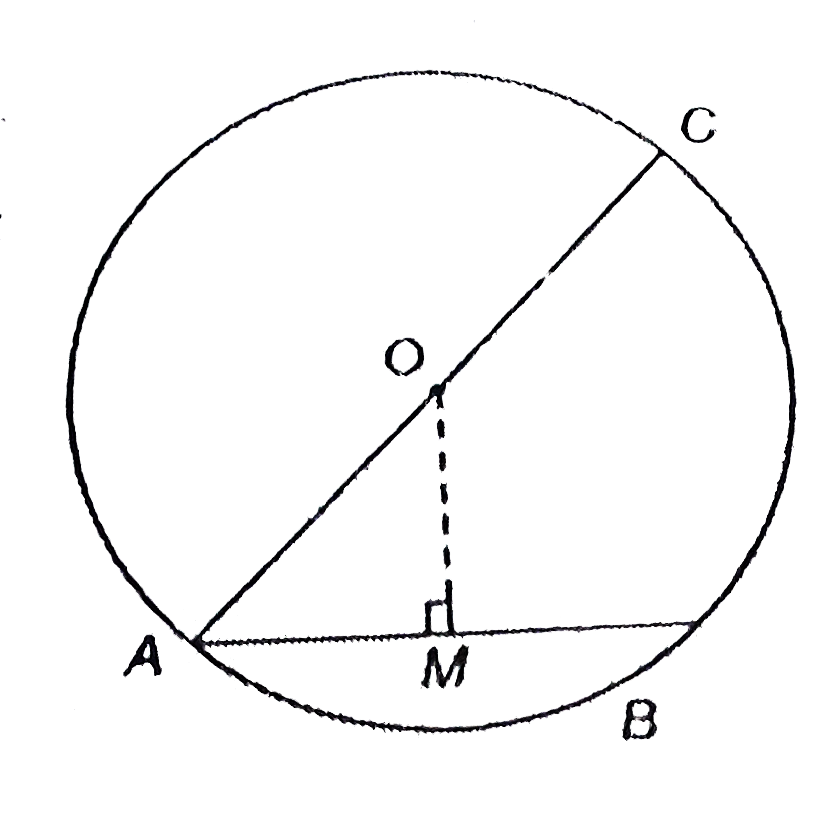
In the adjoining figure, O is the centre of circle and diameter AC=26cm. If chord AB=10cm, then the distance between chord AB and centre O of the circle is :
 A24 cmB16 cmC12 cmDnone of the above
A24 cmB16 cmC12 cmDnone of the aboveIn the adjoining figure O is the centre of the circle . If chord AB=2 cm radius OA=2 cm, then find the value of ∠ACB.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘The length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
A6 cmB5 cmC8 cmD7 cm
O is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
View SolutionA chord of length 16cm is drawn in a circle of radius 10cm. Find the distnace of the chord from the centre of the circle.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

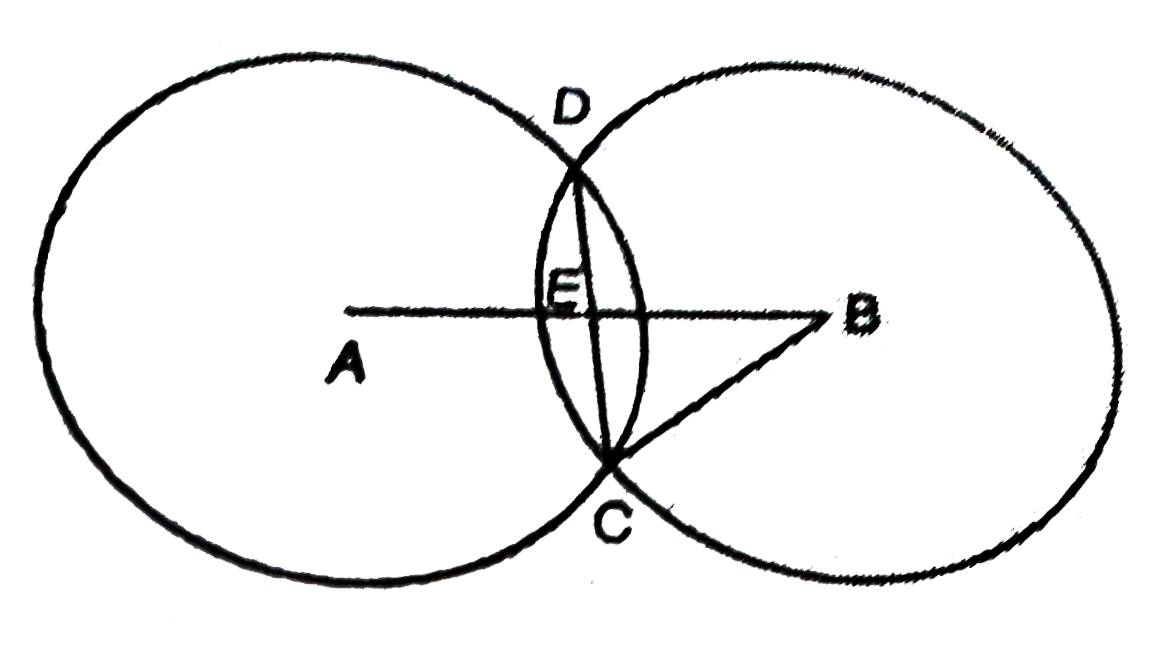
View SolutionIn the adjoining figure, A and B are the centres of two circles. If CB=17cm, EB=15cm, then find the length of common chord.
View SolutionA chord of length 16 cm is drawn in a circle of radius 10 cm .Calculate the distance of the chord from the centre of the circle.
View Solution