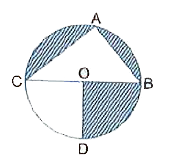
In the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90∘. Find the area of the shaded region.
Since O is the centre of circle
∴ BC is the diameter of circle
∴∠CAB=90∘
(angle in a semicircle is right angle)
Now in right ΔACB, by Pythagoras theroem,
BC2=AC2+AB2+(24)2+(7)2=576+49=625
∴BC=√625=25m
∴ Diameter of circle = 25 m
∴ Radius of circle =252=12.5m
∴OC=OD=12.5m
∴ Area of shaded region = area of circle −ar(ΔABC)−ar(sectorCOD)
=π(12.5)2−12×AC×AB−π(OC)2×90∘360∘

=227×12.5×12.5−12×24×7−227×12.5×12.5×14
=491.07−84−122.768=284.302=284.30m2 (approx)
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Problems From NCERT /exemplar25videos
AREA RELATED TO CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A25videos
AREA RELATED TO CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
Similar Questions
In the given Fig, O is the centre of the circle with AC=24cm,AB=7cmand∠BOD=90∘. Find the area of the shaded region [Take π=3.14 ]
 View Solution
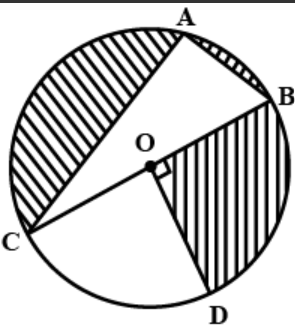
View SolutionIn Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]
 View Solution
View SolutionIn the given figure O is the centre of the circle with AC=24cm,AB=7cm and ∠BOD=90∘. Find the area of shaded region.
[Use π=3.14]
 View Solution
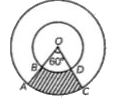
View SolutionIn the figure, the radii of two concentric circles with centre O are 7 cm and 14 cm and ∠AOC=60∘. Find the area of the shaded region.
 View Solution
View SolutionIn the adjoining figure, two concentric circle with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘, find the area of the shaded region. (Use π=227)
 View Solution
View SolutionIn figure , O is the centre of a circle such that diameter AB= 13 cm and AC = 12 cm . BC is joined .find the area of the shaded region .
 View Solution
View SolutionIn the adjoining figure, if O is the centre of the circle, PQ is a chord, ∠POQ=90∘, area of shaded region is 114 cm2, find the radius of the circle. (π=227)
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.
 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle.
m(arc PQR) =60∘ OP=10 cm
Find the area of the shaded region.

Given θ=60∘,r=10cm
π=3.14,√3=1.73
To find: A(shaded region)View SolutionIn the given figure, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB=60∘, Find the area of the shaded region
 View Solution
View Solution
