
In the diagram as shown, a circle is drawn with centre and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals where .
Area of triangle OPR when is
none of these
The correct Answer is:B
For , equation of PR is .
Area of
Topper's Solved these Questions
Similar Questions
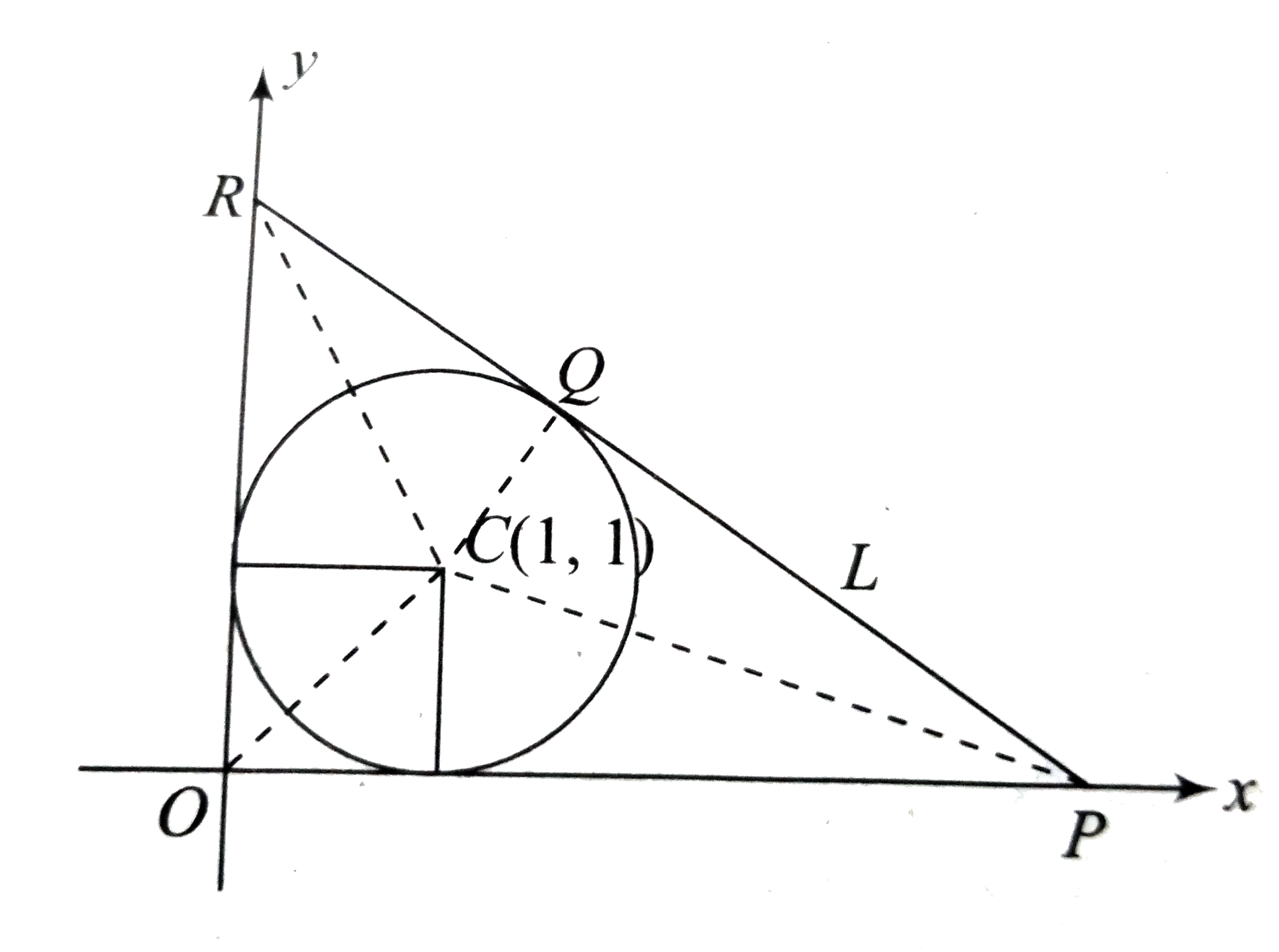
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Equation of the line PR is
View SolutionIf cosθ−sinθ=15, where 0<θ<π4, then

View SolutionIf |z−i|=1 and arg (z) =θ where 0<θ<π2, then cotθ−2z equals
View SolutionA line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View SolutionTangents drawn to circle (x−1)2+(y−1)2=5at point P meets the line 2x+y+6=0 at Q on the x axis. Length PQ is equal to
View SolutionConsider with circle S:x2+y2−4x−1=0 and the line L:y=3x−1. If the line L cuts the circle at A and B then Length of the chord AB is
View SolutionThe line 2x - y + 1 = 0 is tangent to the circle at the point (2,5) and the centre of the circles lies on x-2y = 4. The radius of the circle is :
View SolutionIf a line, y = mx + c is a tangent to the circle, (x−1)2+y2=1 and it is perpendicular to a line L1 , where L1 is the tangent to the circle x2+y2=8 at the point (2, 2), then :
View Solutionif the tangent to the curve x=a(θ+sinθ),y=a(1+cosθ) at θ=π3 makes an angle α x=axis then α
View SolutionTo the circle x2+y2+8x−4y+4=0 tangent at the point θ=π4 is
View Solution
