
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Area of triangle OPR when θ=π/4 is
(3−2√2)
(3+2√2)
(6+4√2)
none of these
The correct Answer is:B
For θ=π/4, equation of PR is x+y=2+√2.
⇒ Area of ΔOPR=12(2+√2)2=(3+2√2)
Topper's Solved these Questions
Similar Questions
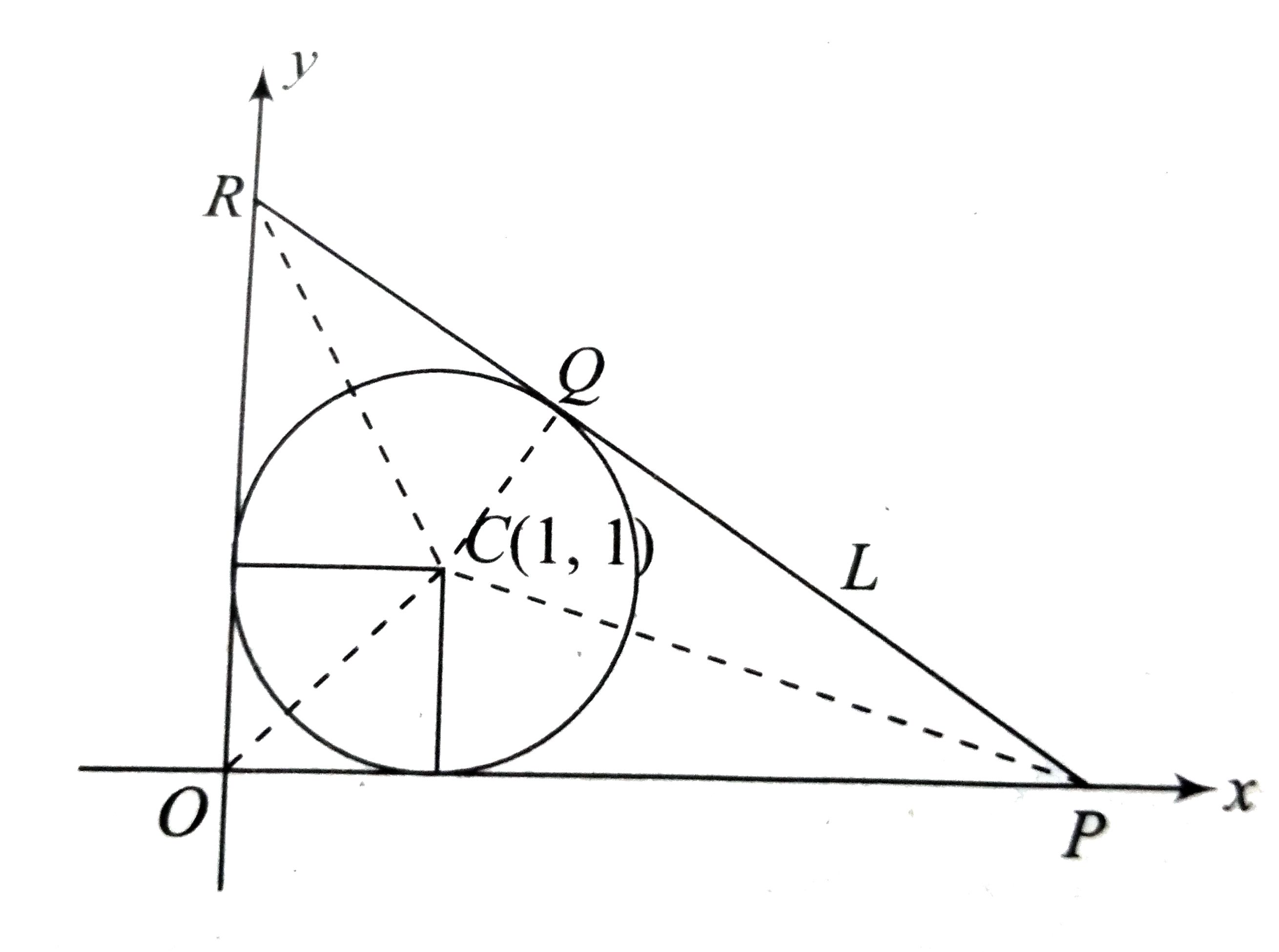
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Equation of the line PR isView SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
View Solution
Knowledge Check
- Question 1 - Select One

In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Equation of the line PR isAxcosθ+ysinθ=sinθ+cosθ+1Bxsinθ+ycosθ=cosθ+sinθ−1Cxsinθ+ycosθ=cosθ+sinθ+1Dxtanθ+y=1+cot(θ2) - Question 2 - Select One
If 5cos2θ+2cos2θ2+1=0, where 0<θ<π, then the values of θ are
Aπ3±πBπ3,cos−1(35)Ccos−1(35)±πDπ3,π−cos−1(35) - Question 3 - Select One
If sinθ+2cosθ=−1, where 0<θ<π2, what is 2sinθ−cosθequal to ?
A−1B12C2D1
If cosθ−sinθ=15, where 0<θ<π4, then
 View Solution
View SolutionIf sinθ+2cosθ=1, where 0<θ<π2, then what is 2sinθ−cosθ equal to ?
View SolutionIf 0<θ<π4, then what is √1−2sinθcosθ equal to ?
View SolutionIf sinθ+cosθ=1+√32, where 0<θ<π2, then what is tanθ+cotθ equal to ?
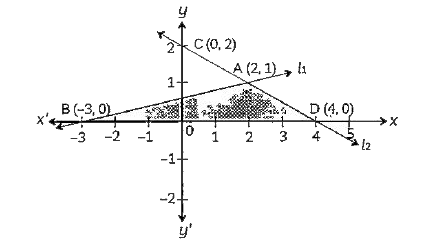
View SolutionThe area of triangle formed by the lines l1andl2 and the x-axis is:
 View Solution
View Solution
