In the figure a disc is shown on which a player spins on arrow twice. The fraction ab is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on the second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction ab>1.
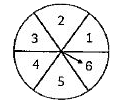
The correct Answer is:512
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - EDUCART PUBLICATIONCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
19 Videos
- STATISTICS AND PROBABILITYBOOK - EDUCART PUBLICATIONCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS (SA-I) Type Questions
45 Videos
- SAMPLE QUESTION PAPER 02BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE QUESTION PAPER 02EXERCISE - SECTION - D
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
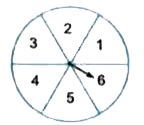
In Fig., shown a disc on which a player spins an arrow twice. The function ab is formed, where 'a' is the number of sector on which arrow stops on the first spin and 'b' is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction ab>1.
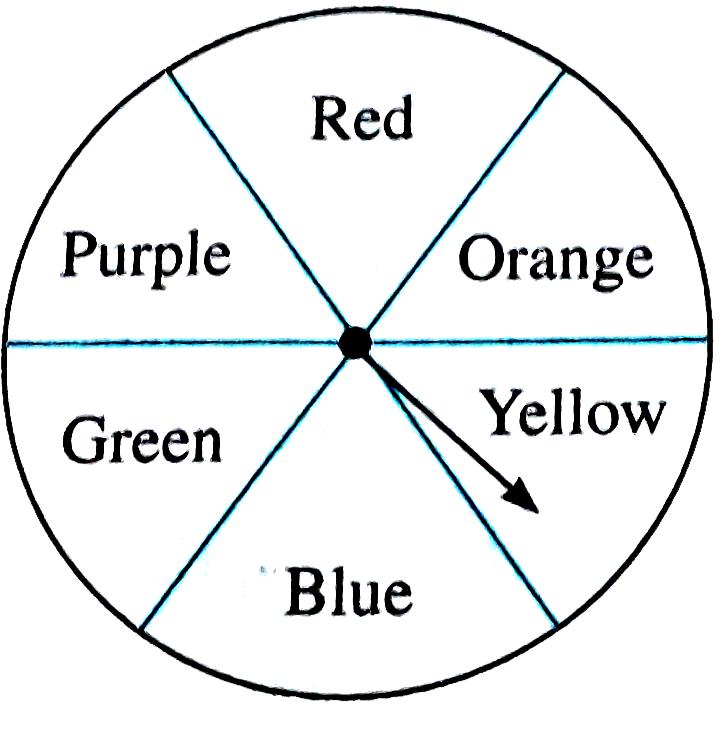
View SolutionThe arrow is rotated and it stops randomly on the disc. Find out on which colour it may stop.
View Solution
Knowledge Check
If you have a spinning wheel with 3 gree sectors, 5 black sectors and 10 red secton then the probability of getting a non-black Sector, is :
A19B16C59D1318A game of chance consists of spinning an arrow, which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
A58B78C18D38
" Which of the following is significance of spin quantum number "
View SolutionIn a spinning wheal, there are 3 red and 4 green sectors having equal areas. It is spinned. What is the probability of getting a redsector ?
View SolutionSuppose you spin the wheel List the number of outcomes of getting a green sector and not getting a green sector on this wheel (i) Find the probability of getting a green sector (ii) Find the probability of not getting a green sector.
View SolutionWhen you spin the wheel shown, what are the possible outcomes. (see figure, outcome here means the sector at which the pointer stops)
View SolutionState True or False:
The probability of the spinning arrow stopping in the shaded region is 12

View SolutionIf you have a spinning wheel with 3-green sectors, 1-blue sector and 1-red sector. What is the probability of getting a green sector? Is it the maximum?
View Solution
