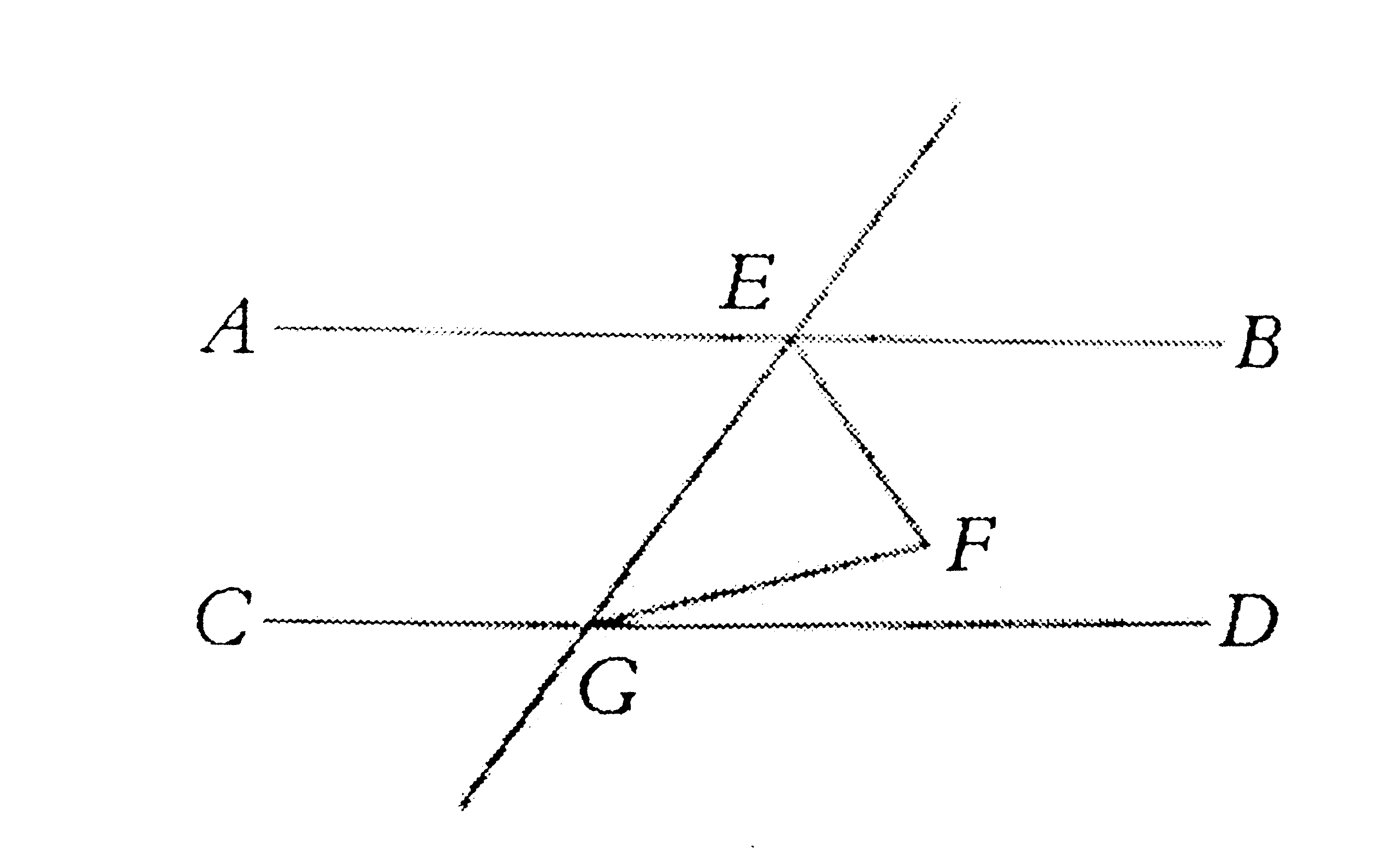
In the figure above, AB || CD. EF and FG are the bisectors of , respectively. . Find .
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
EF and FG bisect respectively.
(1)
(2)
On solving Eq. (1) and (2), we get .
Hence, the correct option is ( c).
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-1
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-2
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-2
26 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check

In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.A20∘B25∘C40∘D35∘In the figure , AB||CD, EG & FG are Bi sectors of ∠BEF & ∠DFE respectively , the m∠FGE is -
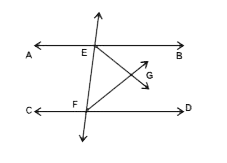 A45∘B90∘C60∘D100∘
A45∘B90∘C60∘D100∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘
In the given figure AB||CD and EF||DQ. Find the value of ∠DEF.
View SolutionIn the given figure AB||CD||EF then find the value of x
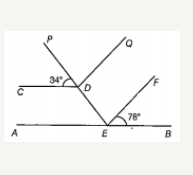
View SolutionIn the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
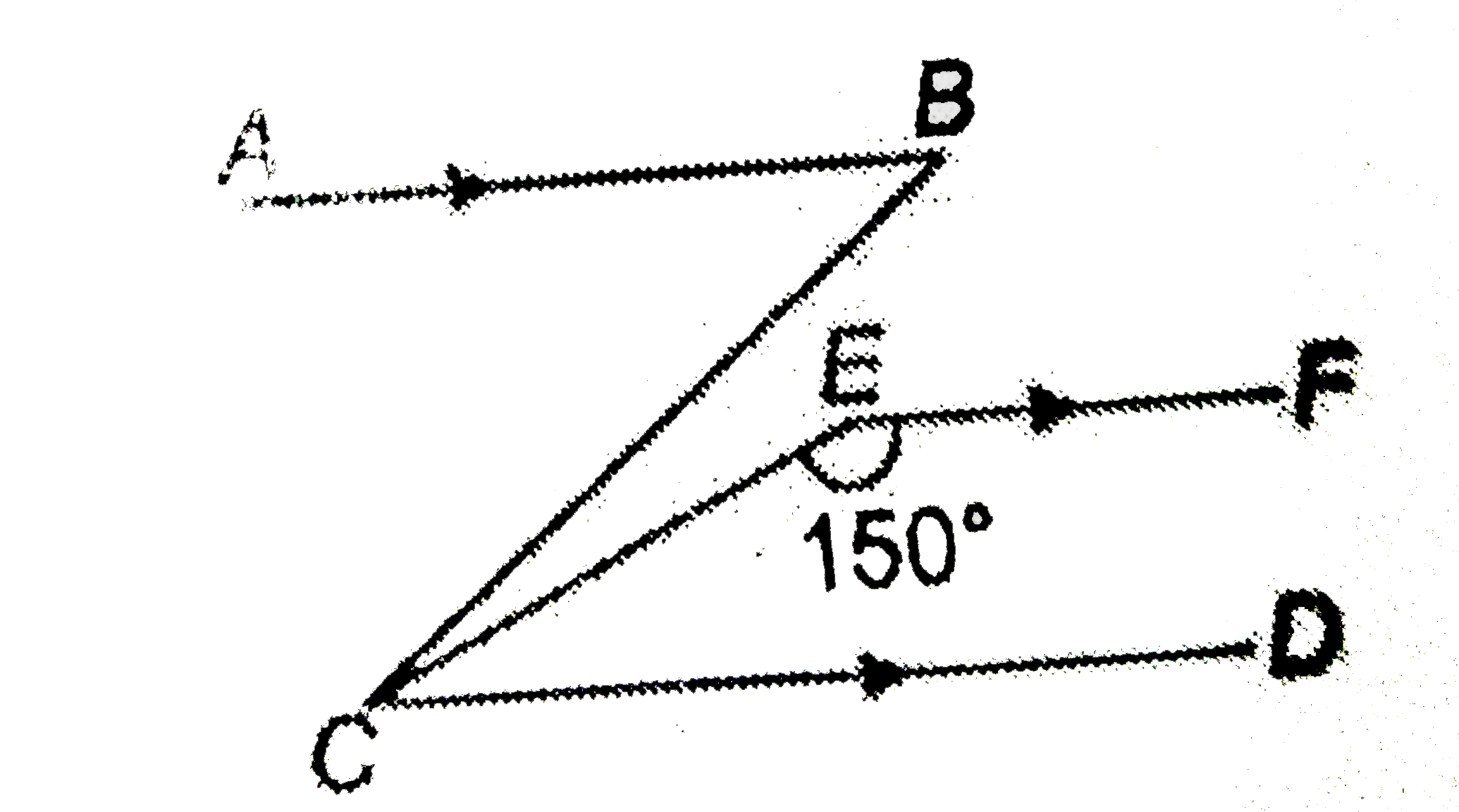
View SolutionIn the given figure AB||CDandEF||DQ. Find the value of ∠DEF:
View SolutionThe straight lines AB and CD intersect at E . If EF and EG are bisectors of ∠DEAand∠AEC respectively and if ∠AEF=xand∠AEG=y , then
View Solution

