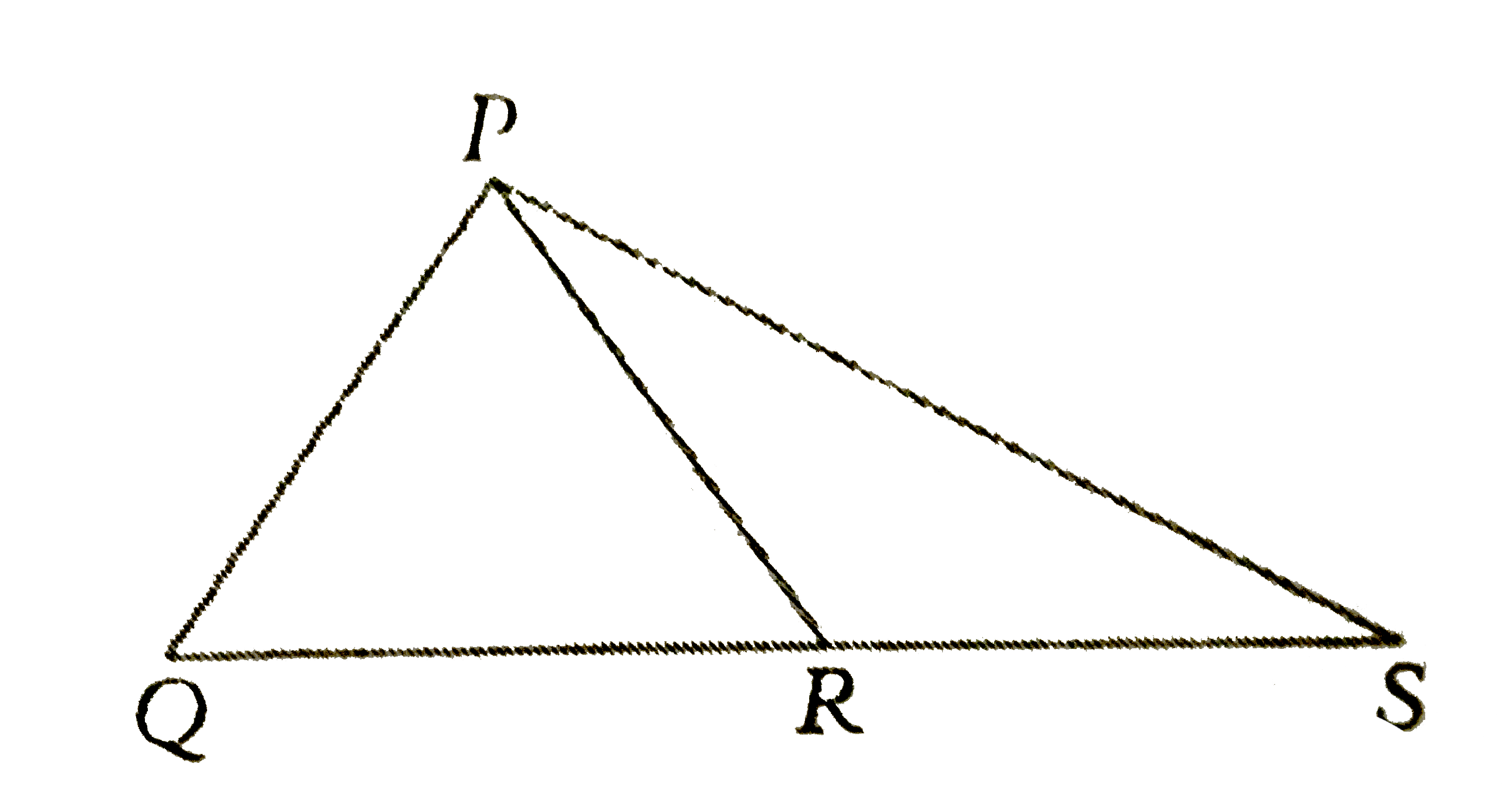
In the figure above, ∠QPS=2∠SPR,∠Q=∠R+40∘,and∠PSR=120∘. Find ∠QPR.
A
50∘
B
55∘
C
65∘
D
60∘
Video Solution
Text Solution
The correct Answer is:D
From the figure , in ΔPSR,x+y=60∘ ( ∵∠PSR=120∘)
⇒y=60∘−x (1)
In ΔPQS,2x+y+40∘=120∘ .
2x+60∘−x+40∘=120 ( from Eq.(1))
x=20∘
∴∠QPR=3x=3×20∘=60∘
Hence, the correct option is (d) .
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-1
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-2
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-2
26 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check
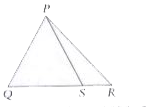
In the figure above ∠QPS=2∠SPR,∠Q=∠R+40∘and∠PSR=120∘. Find ∠QPRA50∘B55∘C65∘D60∘In the given figure, ∠CAB=40∘and∠AKB=105∘. Find ∠KCD :
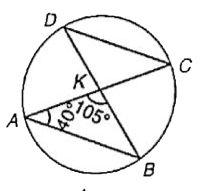A65∘B35∘C40∘D72∘
In the figure above, ∠SPT=60∘and PQ=PR. Find ∠PQR
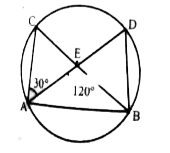
View SolutionIn the figure, ∠CAE=30∘and∠AEB=120∘. Find ∠ADB
View Solution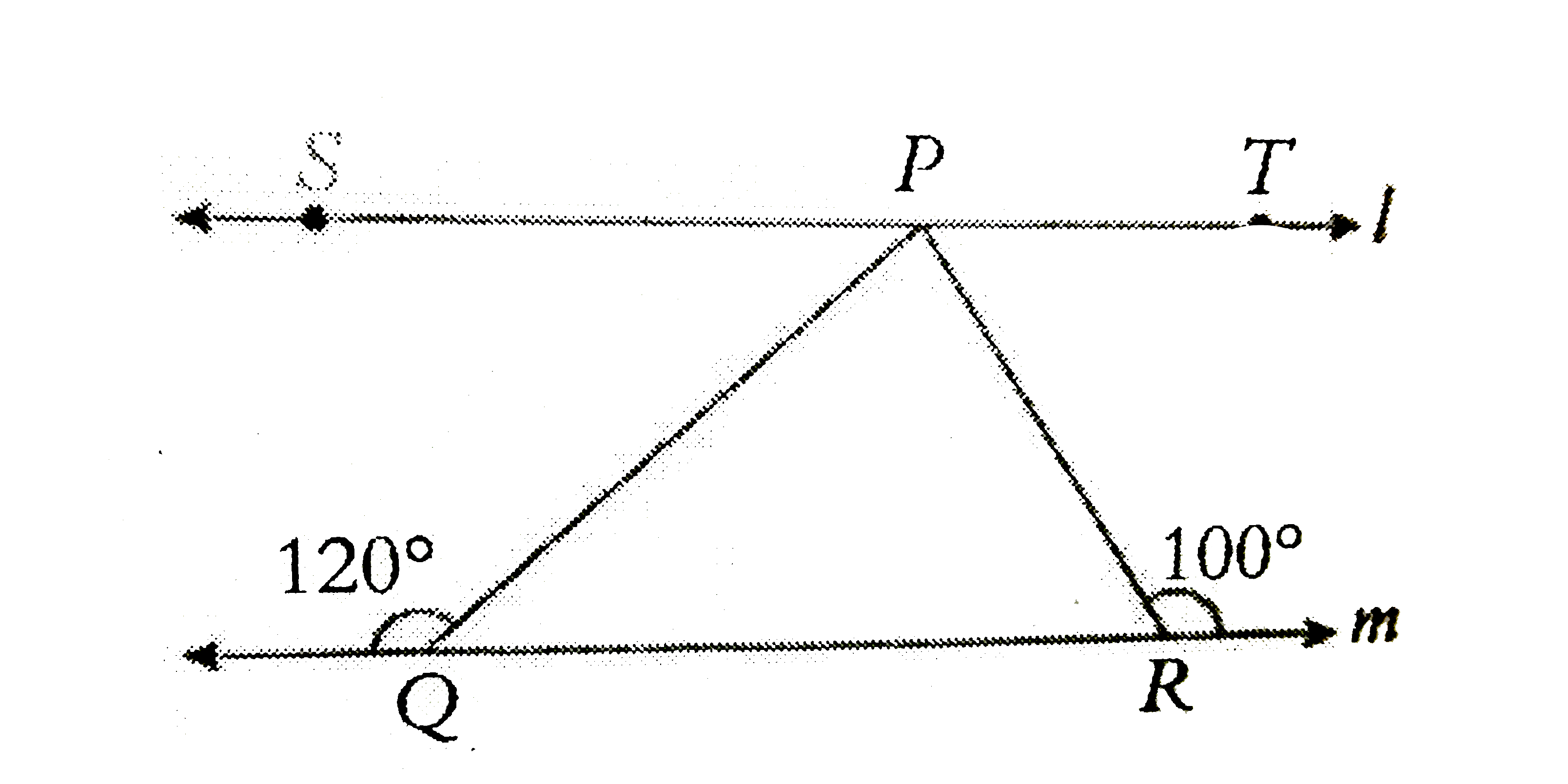
In the figure above, if l//m, then find ∠QPS+∠RPT.
View Solution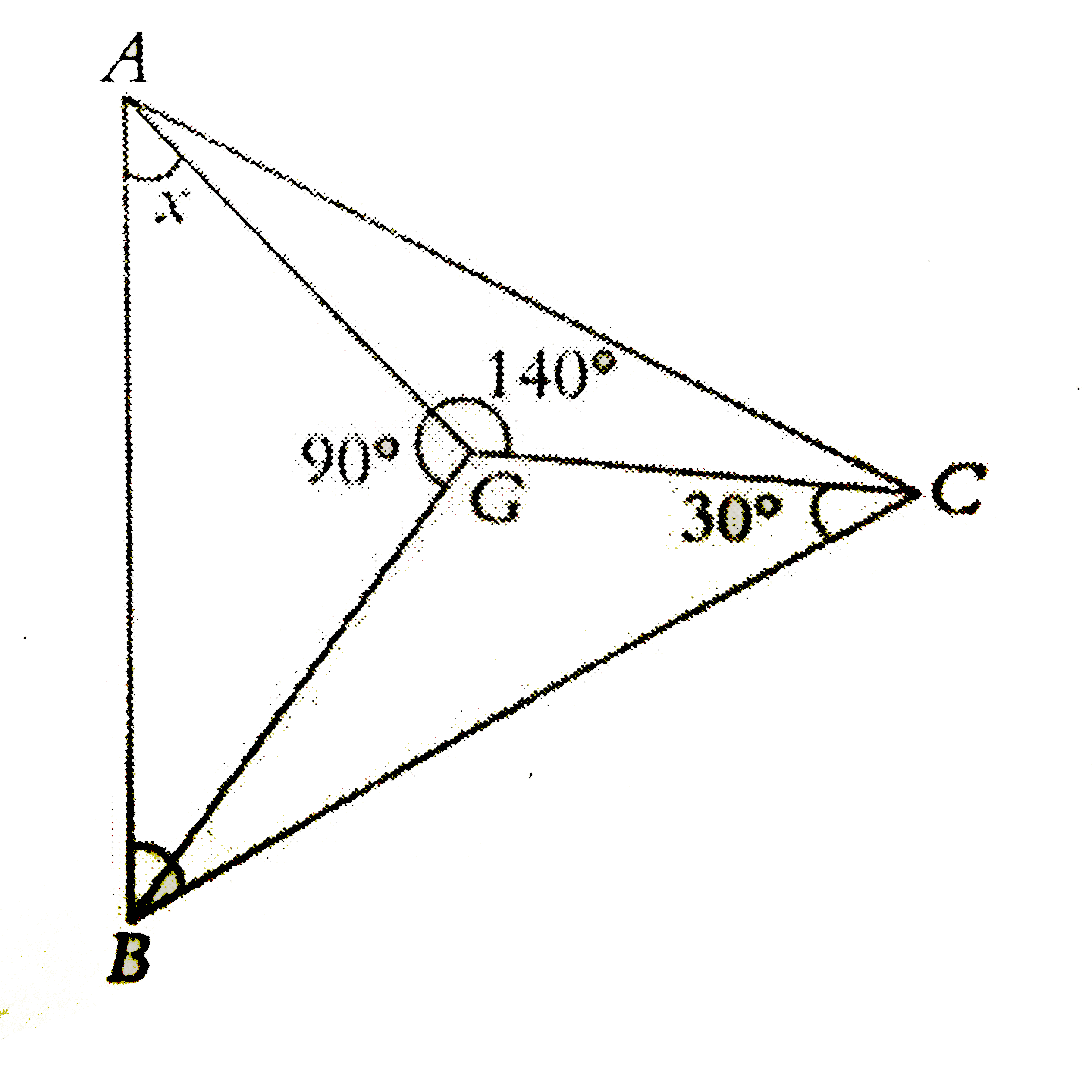
In the figure above, ∠ABC=60∘. Find x.
View Solution
In the figure above, PQRS is a square , ∠PTR=110∘, then find ∠TPS.
View Solution-
In the figure above, PQRS is a square , ∠PTR=110∘, then find ∠TPS.
View Solution