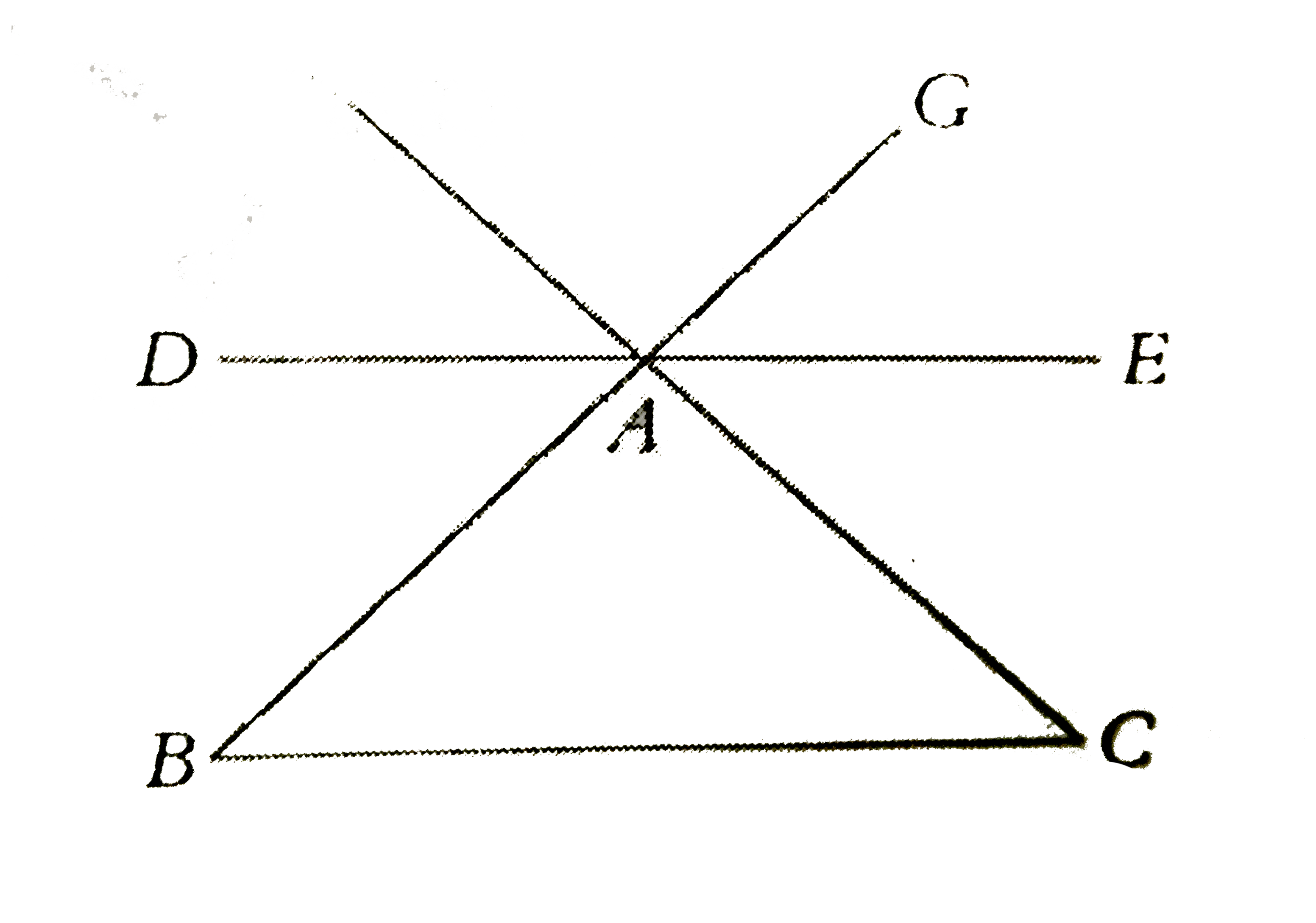
In the figure above ( not to scale ),
DAE||BC, ∠BAD=(2x−20)∘. Find ∠EAC.
A
40∘
B
25∘
C
30∘
D
35∘
Text Solution
The correct Answer is:C
DAE∣∣BC∠DAB=∠ABC( ∴ Alternate interior angles ) and ∠EAC=∠ACB ( ∴ Alternate interior angles)
FAG=∠BAC (Q vertically opposite angles )
⇒∠BAD=∠ABC=(2x−70)∘(given )
Given, ∠BAC=(2x+20)∘and∠ACB=(x−20)∘
∠ABC+∠BAC+∠ACB=180∘
(2x−70)∘+(2x+20)∘+(x−20)∘=180∘
5x∘−70∘=180∘
x∘=50∘⇒∠ACB=(x=20)∘=30∘
⇒∠EAC=30∘(∵∠EAC=∠ACB)
Hence, the correct option is ( c).
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-1
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-2
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-2
26 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check

In the figure above (not to scale)
DAE∣∣BC,∠BAD=(2x−70)∘
∠ACB(x−20)∘and∠FAG=(2x+20)∘. Find ∠EACA40∘B25∘C30∘D35∘In the following figure ( not to scale), ∠ADC=60∘,∠BAD=80∘ and ∠EBC=2∠PDE. Find ∠APE.
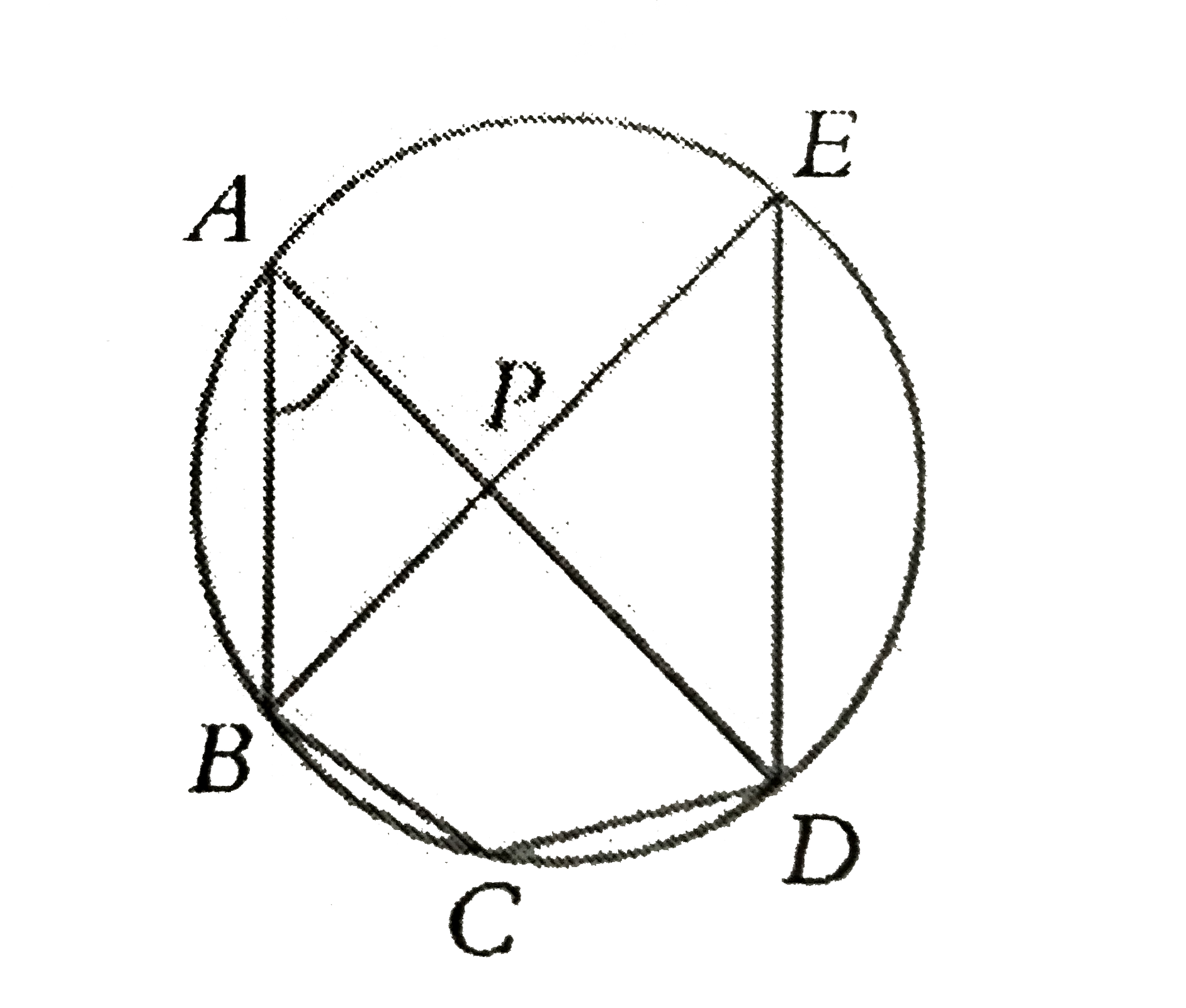 A60∘B80∘C120∘D140∘
A60∘B80∘C120∘D140∘In the figure above (no to scale), l∣∣m and also x:y=5:3. Find the measure of angles (x−40∘) and (y+40∘) respectively.
 A60∘,100∘B60∘,60∘C100∘,60∘D60∘,80∘
A60∘,100∘B60∘,60∘C100∘,60∘D60∘,80∘
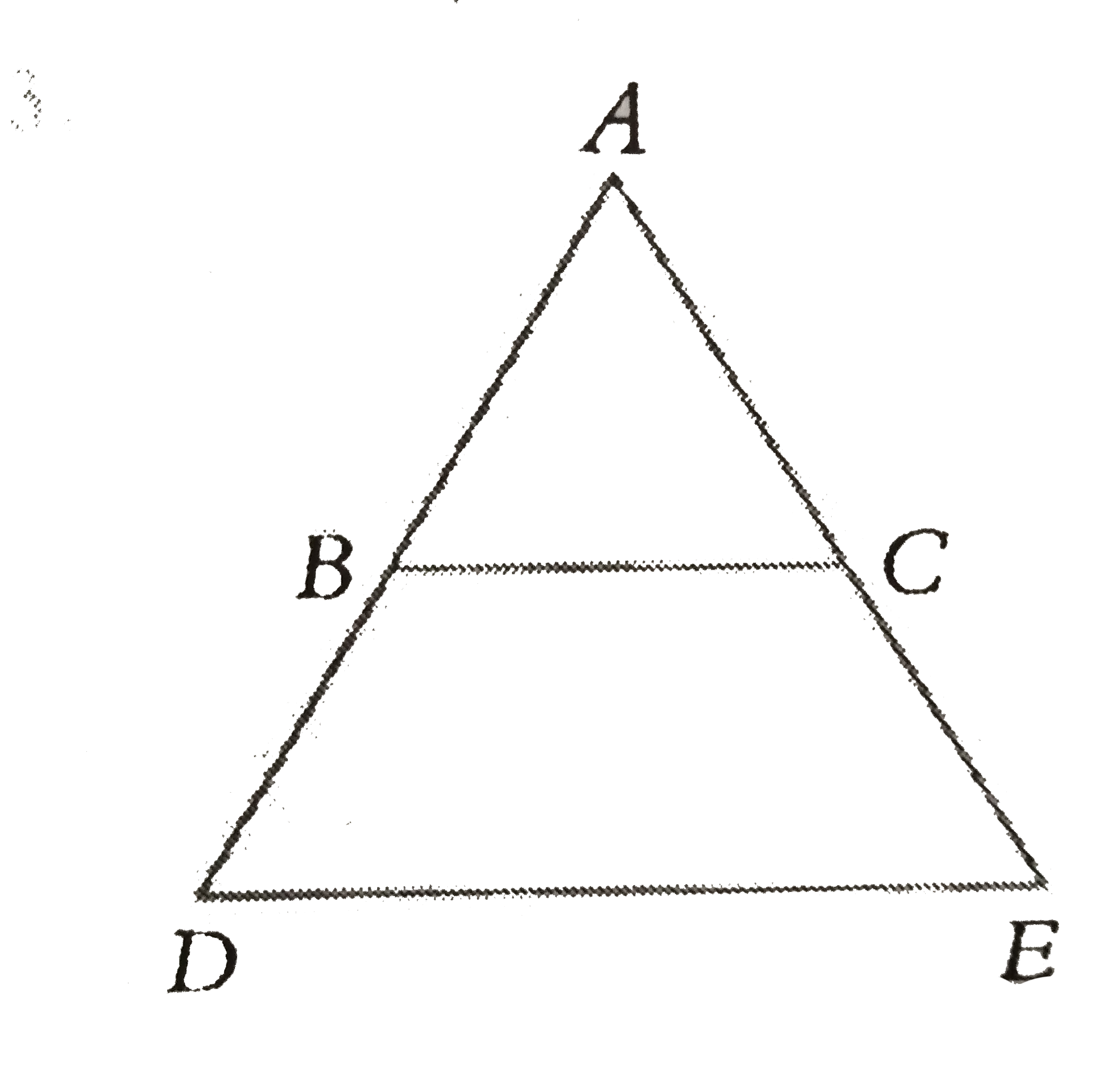
In the figure above, BC || DE and ∠ABC=∠CED.∠A=∠ACB−30∘. Find ∠A.
View Solution
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
View SolutionIn the figure above (no to scale), l∣∣m and also x:y=5:3. Find the measure of angles (x−40∘) and (y+40∘) respectively.

View Solution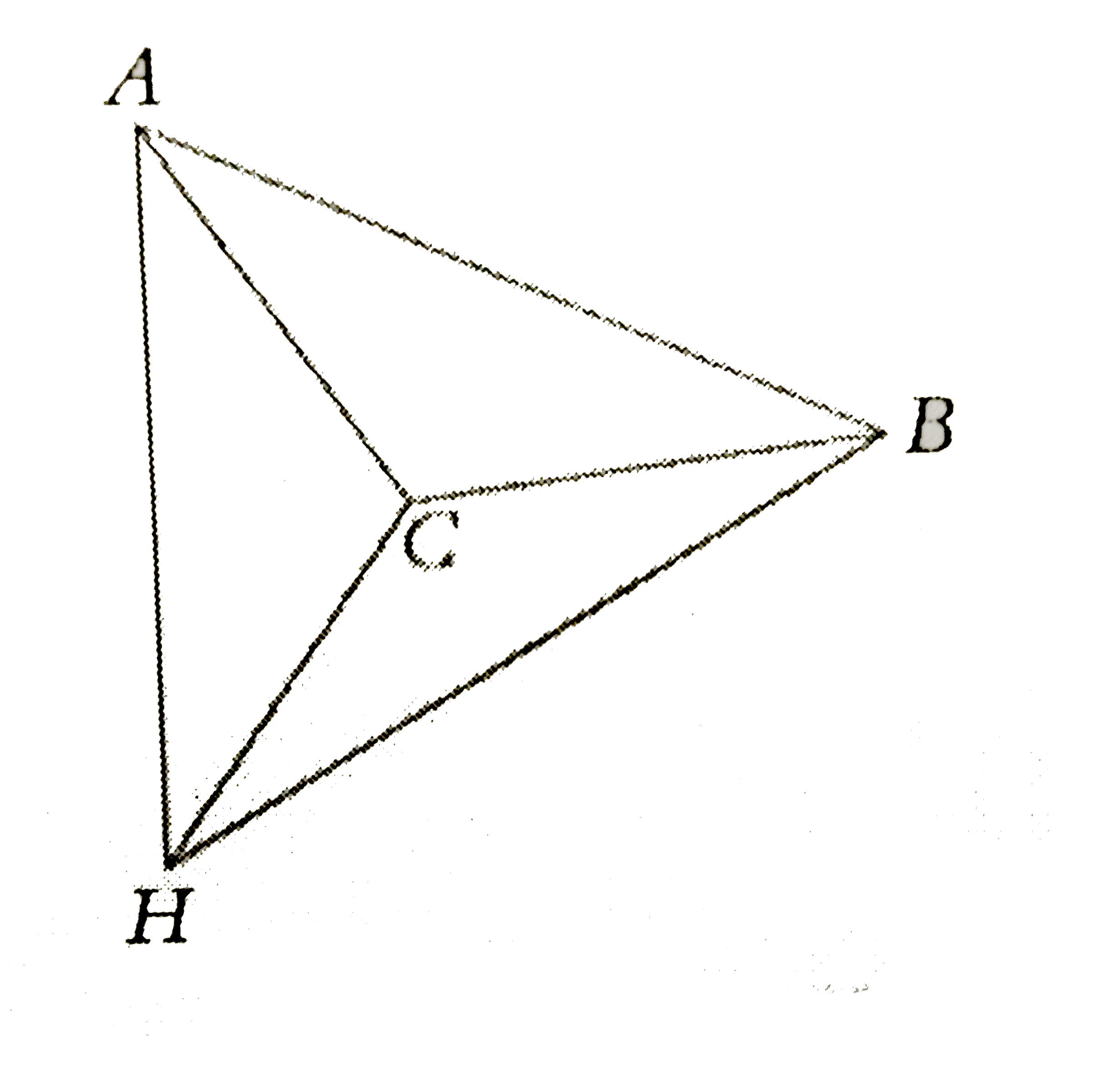
In the figure above ( not to scale ), ΔACB≅ΔACH≅ΔBCH. Find ∠BCH.
View Solution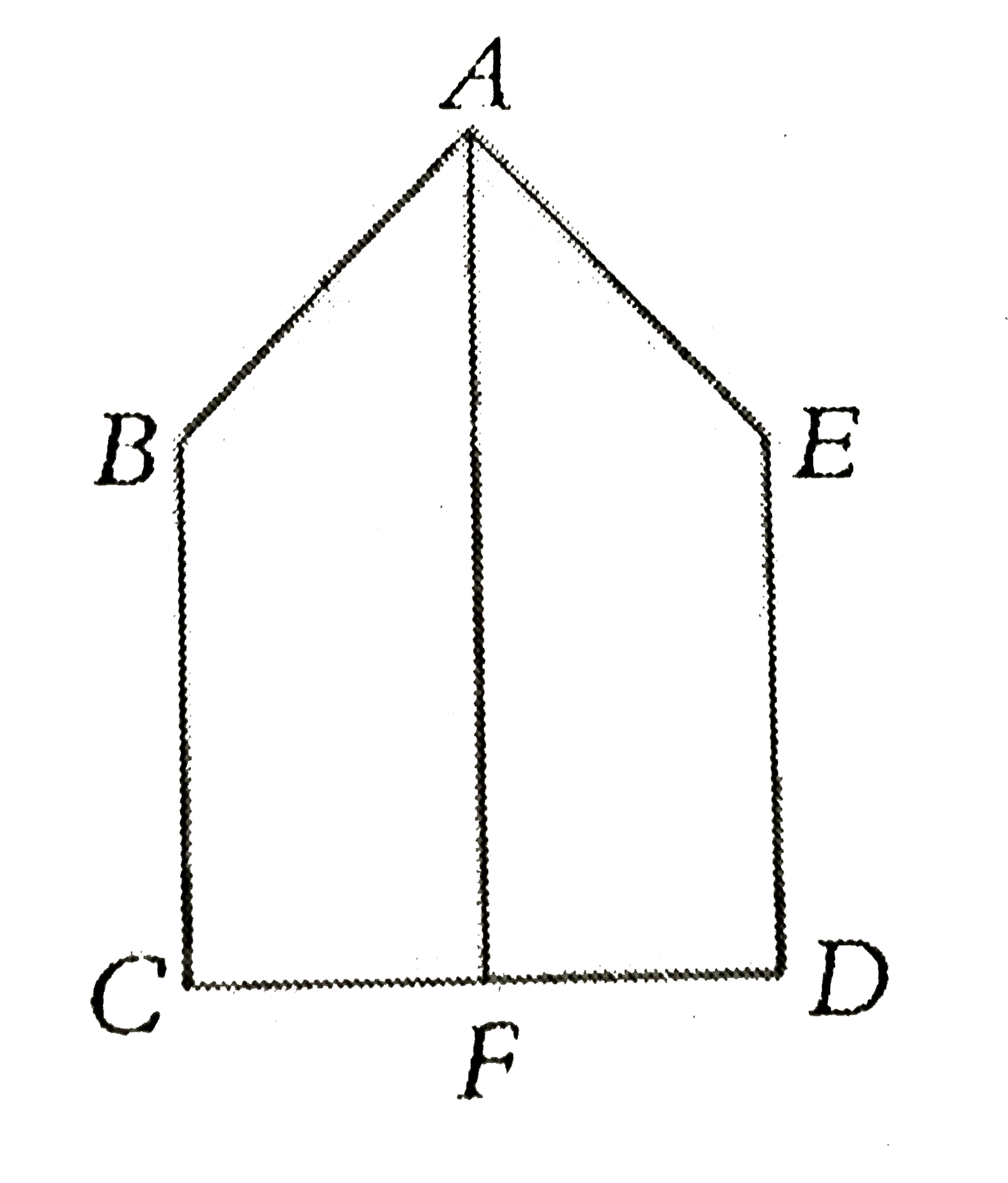
In the figure above (not to scale), ABCDE is symmetrical about AF. If ∠C=90∘ and ∠BAF=45∘, then find the ∠E.
View Solution

