In the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
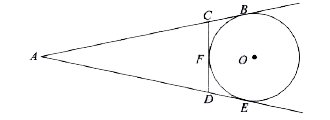
AD=AB+BC+CA
2AD=AB+BC+CA
AD2=AB+BC+CA
AD4=AB+BC+CA
The correct Answer is:B
Topper's Solved these Questions
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - TEST YOURSELF (LEVEL 3)
32 Videos
- STANDARD AND ALLIED ANGLESBOOK - CENGAGECHAPTER - STANDARD AND ALLIED ANGLESEXERCISE - Olympiad And NTSE Level Exercises
10 Videos
- TRANSFORMATIONSBOOK - CENGAGECHAPTER - TRANSFORMATIONSEXERCISE - Olympiad and NTSE level exercises
10 Videos
Similar Questions
In the given figure, chords AD and BC in the circle, are extended to E and F. respectively.
If ∠CDE=85∘,∠DCF=94∘, then the value of ∠ABF+∠EAB is:
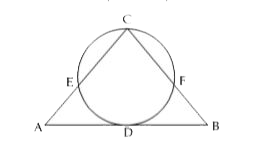
View SolutionABC is an isosciles triangle a circle is such that it parses though vertex C and AB acts as a tangent at D for the same circle AC and BC intersects the circle at E and F respectively AC = BC = 4 cm. and AB = 6 cm. also D is the mid-point of AB. What is the ratio of EC : (AE+AD)?
View Solution
Knowledge Check
BC, AB and AC are tangents to the circle at D, E and F respectively. ∠EBD=x∘,∠FCD=y∘. Then ∠ EDF equals
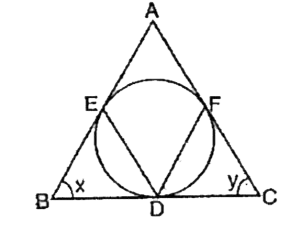 Ax + yBx2−yC90∘−(x+y)Dx+y2
Ax + yBx2−yC90∘−(x+y)Dx+y2ABC is an isosciles triangle a circle is such that it parses though vertex C and AB acts as a tangent at D for the same circle AC and BC intersects the circle at E and F respectively AC = BC = 4 cm. and AB = 6 cm. also D is the mid-point of AB. What is the ratio of EC : (AE+AD)?
 A1:2B1:3C2:5Dnone of these
A1:2B1:3C2:5Dnone of theseIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
In the figure, D E and F are midpoints of sedes AB,BC and AC respectively. P is the foot of the perpendicular from A to side BC. Show that points D, E,F and P are concyclic.

View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionIn the given figure, D, E and F are the points where the incircle of the ΔABC touches F the sides BC, CA and AB respectively. Show that AF+ BD + CE = AE + BF + CD = (perimeter of ΔABC)
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC such that the BDCD,CEAE,AFBF=−1
View Solution
