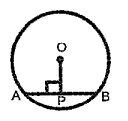
In the figure O is the center. Radius = 5cm. AB = 8 cm. what is the perpendicular distance from the center of the circle to AB.
 Solution in Malayalam
Solution in Malayalam
Step by step video & image solution for In the figure O is the center. Radius = 5cm. AB = 8 cm. what is the perpendicular distance from the center of the circle to AB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
Write the dcimals given below in the fractional form.
0.1203:26View SolutionSum of two numbers is 25. The difference is 10. Find the numbers.
02:11View SolutionIn the given figure (not to scale), O is the centre of the circle. A,B,C and D are concyclic and AB=CD . If /_MON =120^(@) , then find /_ OPN .
01:31View SolutionDetermine the point of symmetry of a regular hexagon.
02:46View SolutionDtermine the images of the following figure about the given line :
02:03View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
02:45View SolutionIn the given figure, AB is a diameter, O is the center of the circle and ∠OCB=50∘ then find ∠DBC.
02:17View SolutionMatch the following Column A to Column B
 05:41View Solution
05:41View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionThe inequation represented by the graph given below is :
02:10View SolutionThe inequation that best describes the graph given below is _________
04:23View SolutionThe inequation that best describes the following graph is _________
02:50View SolutionWhich inequations represent the shaded region in the given figure
02:02View SolutionIn fig. O is the center of the circle. Find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_031_Q01.png" width="80%"gt01:19View SolutionIn the following figure, if O is the center of the circle and ¯¯¯¯¯¯AB is the diameter, then find ∠ACB.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E02_009_Q01.png" width="80%"gt02:41View Solution

