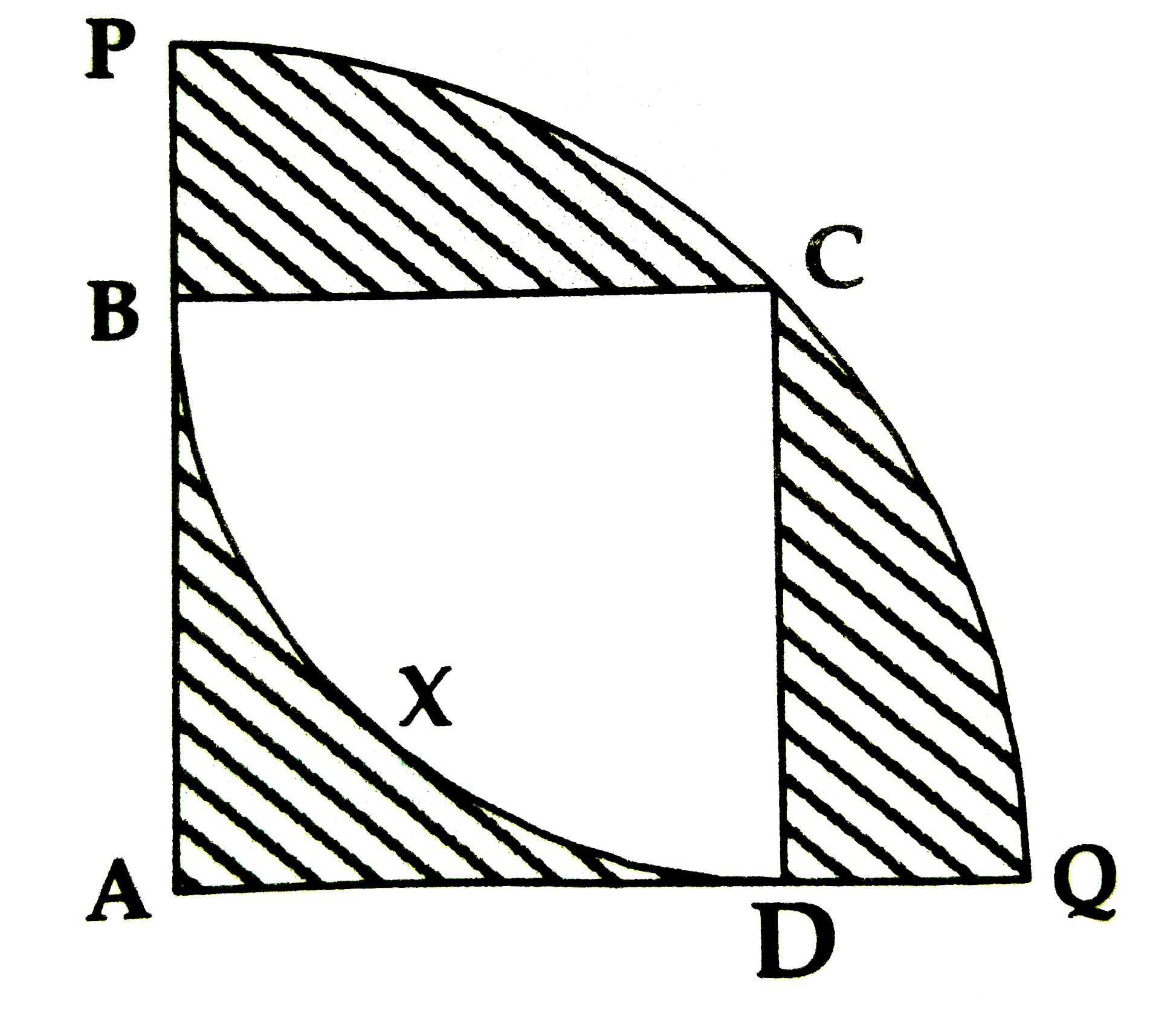
In the figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of the shaded portion.
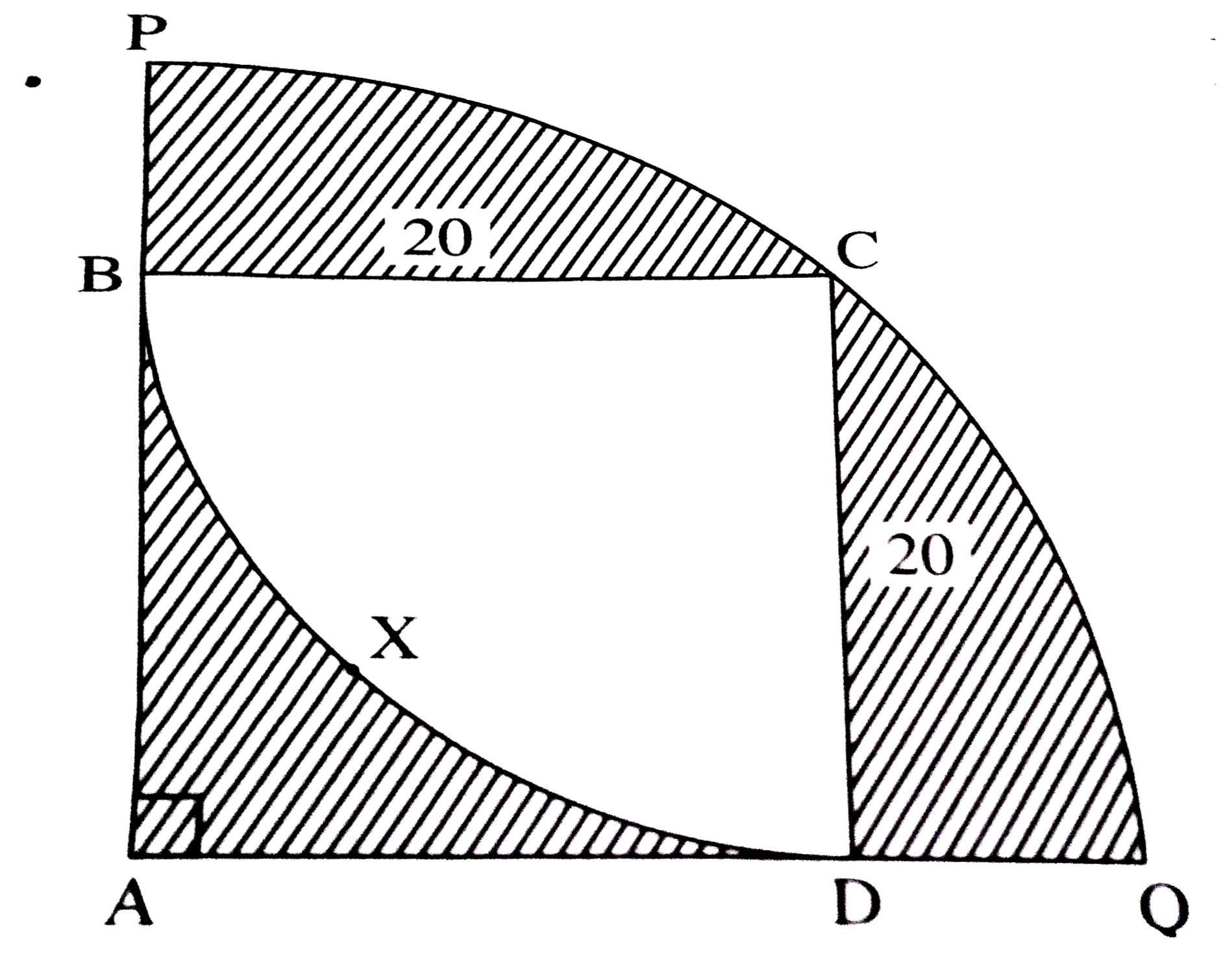
Side of the square ABCD = radius of sector C-BXD = 20 cm
Area of square =side2=400cm2
Area of sector C-BXD =θ360×πr2
=□360×3.14×202=□cm2
Area of the shaded portion inside square
= Area of square - A (sector C- BXD)
=400−□cm2
Radius of sector A-PCQ= Length of diagonal of square ABCD
r1=20√2cm
Area of the shaded region outside square
= A(sector A-PCQ)-A (square ABCD)
=90360×3.14×(20√2)2−200
=□cm2
∴ total area of shaded portion = area of shaded portion inside square + area of shaded portion outside square =□cm2
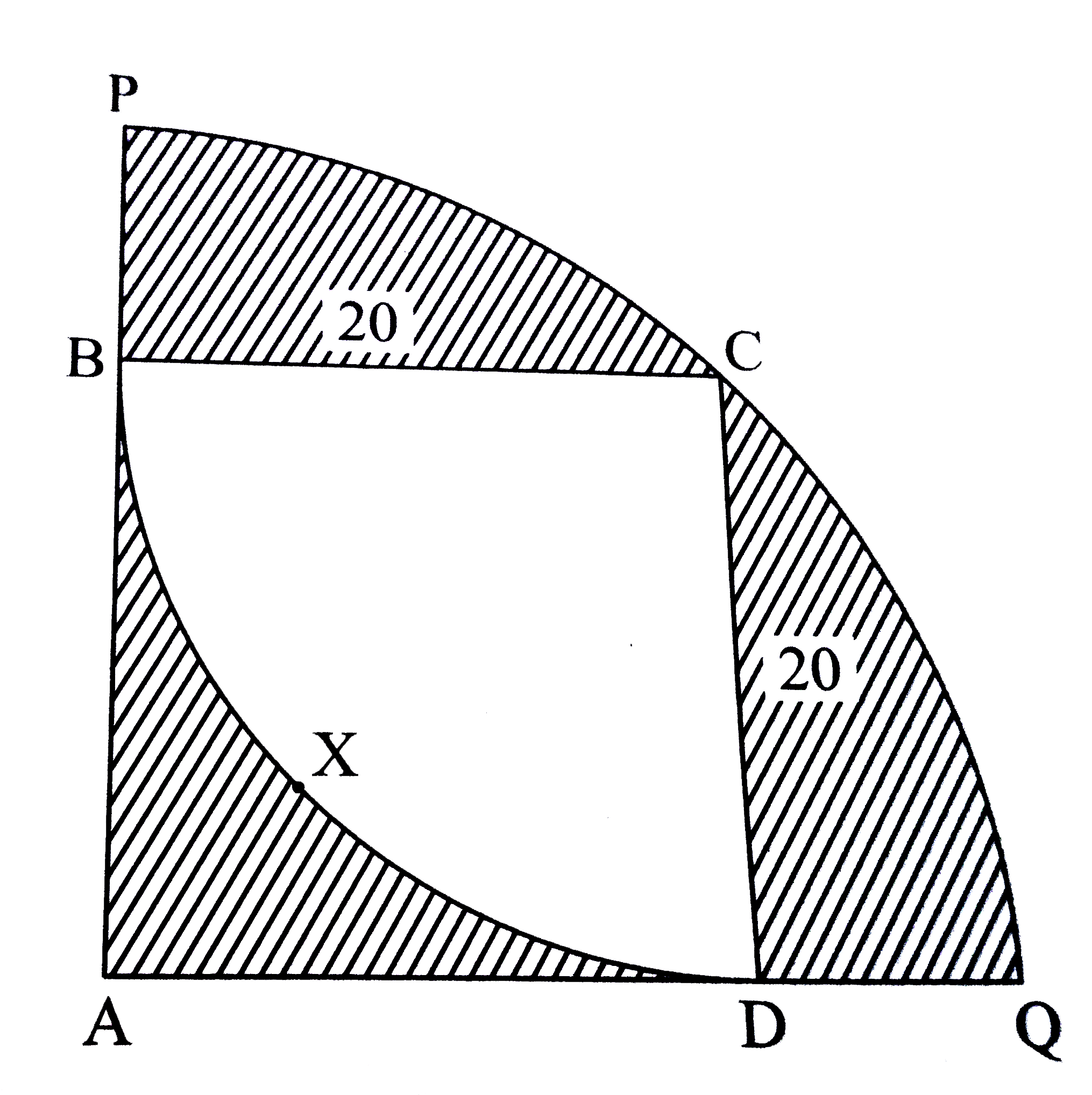
Side of the square ABCD = radius of sector C-BXD= 20 cm
Area of square =side2=400cm2
Area of sector C-BXD=θ360×πr2
=90360×3.14×202
=314cm2
Area of the shaded portion inside square
= Area of square - A (sector C-BXD)
=400−314
=86cm2
Radius of sector A-PCQ = Length fo diagonal of square ABCD
=r1=20√2cm
Area of the shaded region outside square
= A(sector A-PCQ)- A(square ABCD)
=90360×3.14×(20√2)2−200
=228cm2
∴ total area of shaded portion = area of shaded portion inside square + area of shaded portion outside square =314cm2.
Topper's Solved these Questions
- MENSURATIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - 8.5
4 Videos
- MENSURATIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - Assignment 8.1
9 Videos
- MENSURATIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - 8.3
11 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - 4 Marks Questions
18 Videos
- MODEL QUESTION PAPERBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)
2 Videos
Similar Questions
In the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.
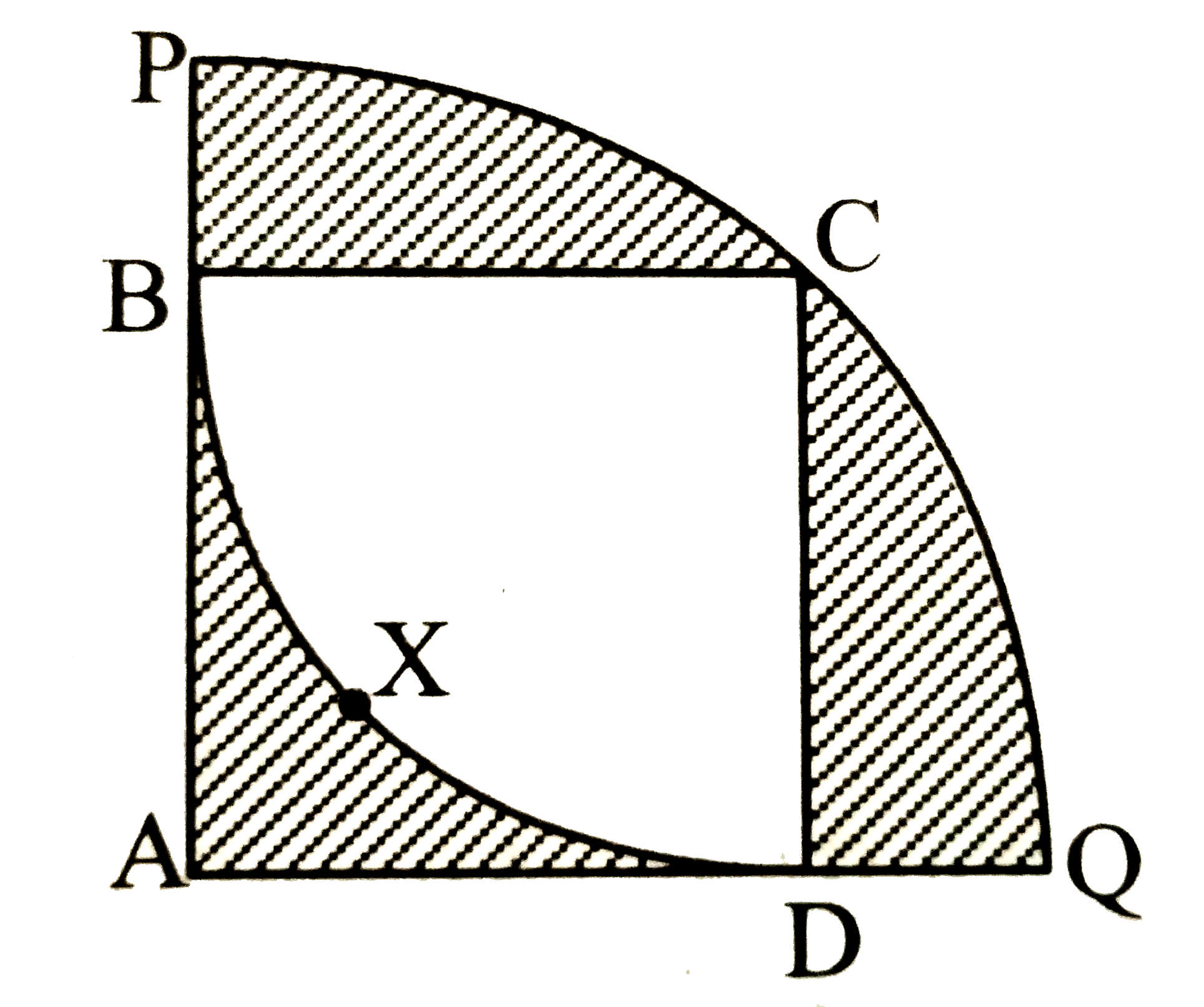
View SolutionIn the figure, square ABCD is inscribed in the sector A-PCQ. The radiuys of sector C-BXD is 20 cm. Find the area of shaded region.
View Solution
Knowledge Check
Find the area of shaded portion if each side of the square is 14 cm.
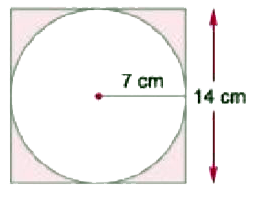 A50 sq cmB45 sq cmC62 sq cmD42 sq cm
A50 sq cmB45 sq cmC62 sq cmD42 sq cm
In the following figure, square ABCD is inscribed in the sector C-BXD IS 20 cm. Complete the following activity to find the area of shaded region
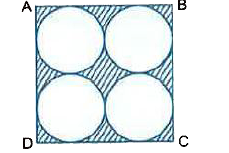
View SolutionFind the area of the shaded region in Fig where ABCD is a square of side 14 cm.
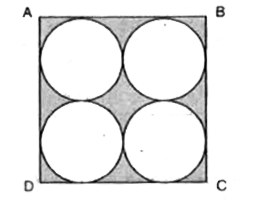
View SolutionFind the area of the shaded region in figure where ABCD is a square of side 14 cm.
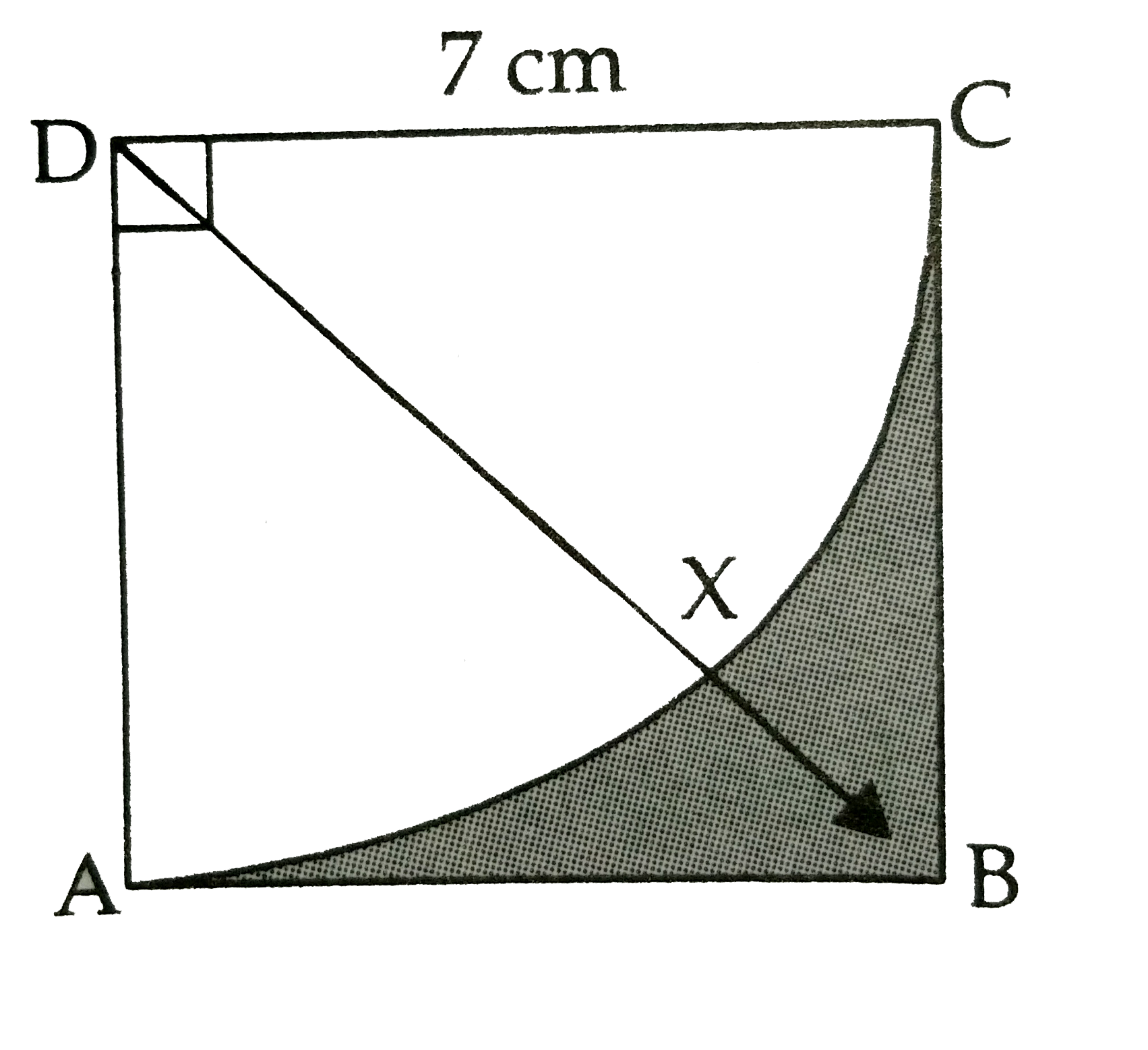
View SolutionIn the given figure, side of square ABCD is 7cm. With centre D and radius DA, sector D-AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region.
View SolutionFind the area of the shaded region in Fig. 12.16, where ABCD is a square of side 14 cm.
View SolutionIn the given figure side of square ABCD is 7 cm.
With centre D and radius DA, sector D-AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region.
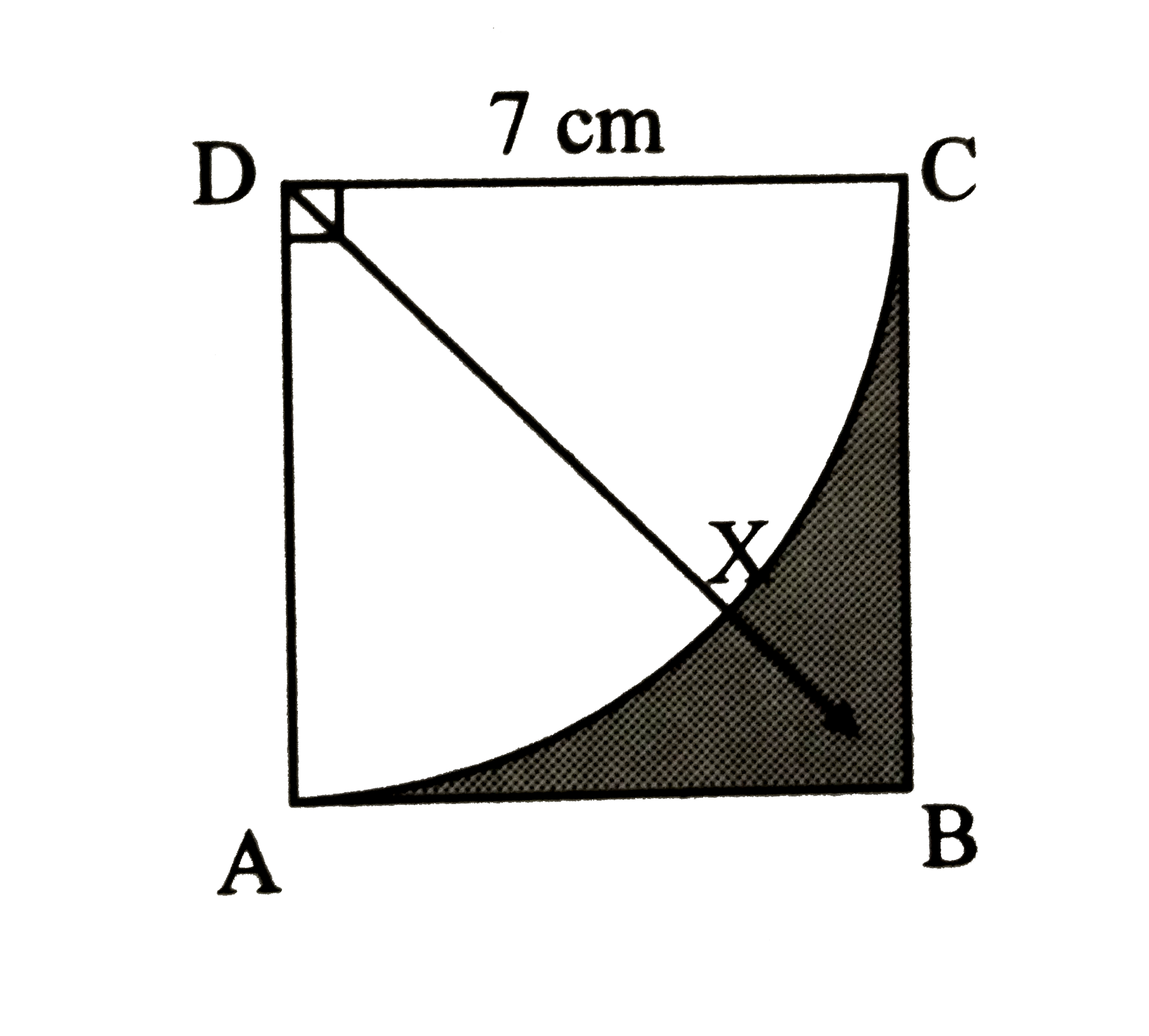
View SolutionFind the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
View Solution
