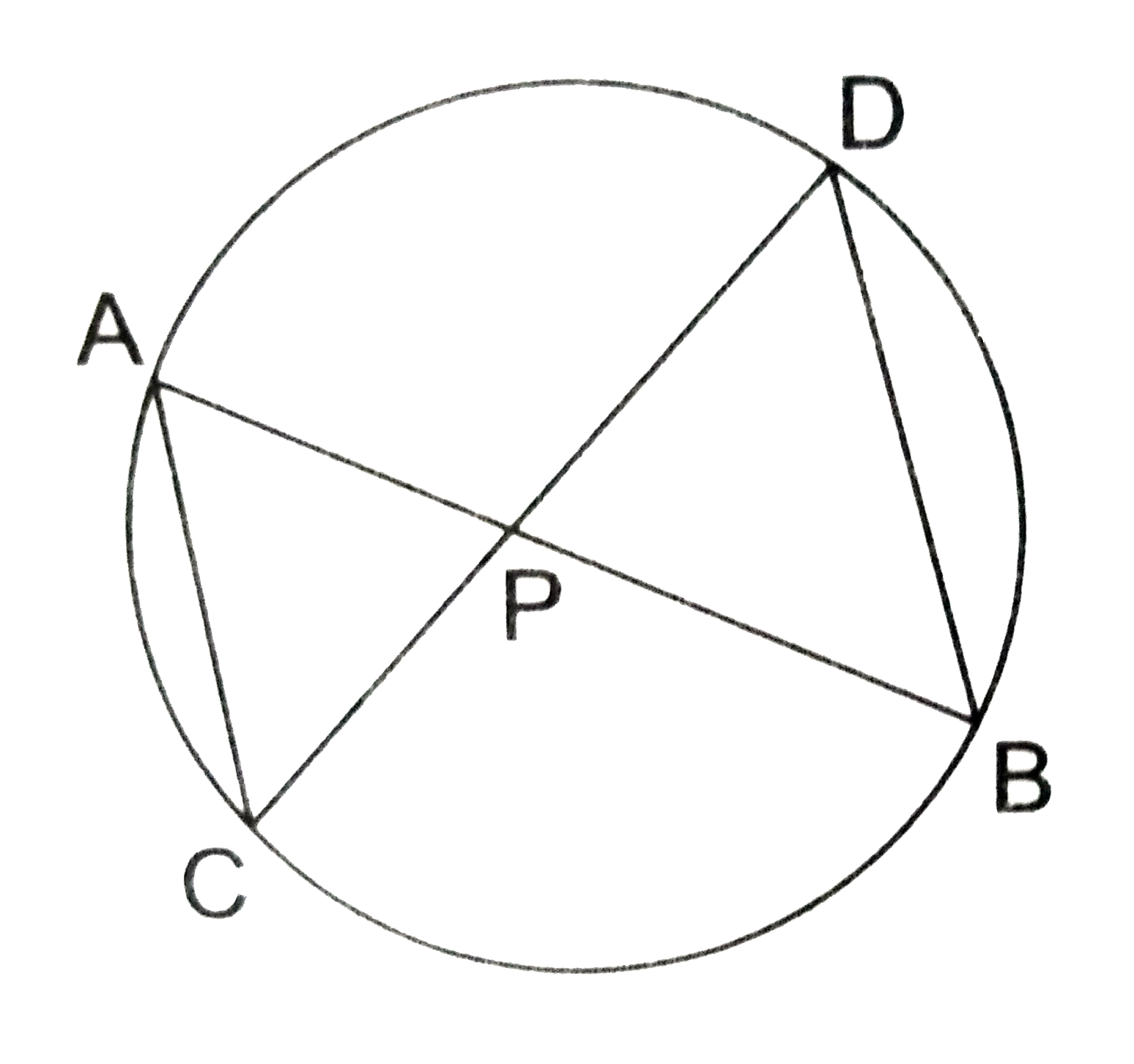
In the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB

Step by step video & image solution for In the figure, two chords AB and CD intersect each other at the point P. Prove that : DeltaAPC ~ DeltaDPB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART - A (SECTION - I)
21 Videos
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART - A (SECTION - II)
5 Videos
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART B (SECTION-IV)
6 Videos
- SAMPLE PAPER 11 (SELF - ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11 (SELF - ASSESSMENT)EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - D
9 Videos
Similar Questions
Knowledge Check
Vinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
AA) 10BB) 18CC) 12DD) 15
In a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
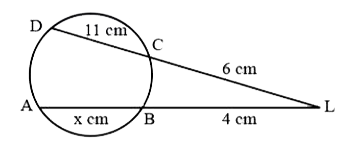
View SolutionIn the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

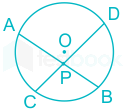
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
View SolutionIn trapezium AC and BD intersect each other at point P. Then prove that A(ΔABP)A(ΔCPD)=AB2CD2.
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA.PB=PC.PD

View Solution


