In the following figure, find the locus of centroid of triangle PAB, where AP perpendicular to PB.

∴ Slope of AP =2t
⇒ Slope of BP =−t2
So, equation of line BP is y−2t=−t2(x−t2).
Putting y = 0, we get point B as (t2+4,0). Now , let centroid of ΔPAB be (h,k).
∴ h=t2+t2+43andk=2t3
Eliminating 't', we get
3h−4=2(3k2)2
∴ 3x−4=9y22, which is the required locus.
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - ILLUSTRATION 5.13
1 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - ILLUSTRATION 5.14
2 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - ILLUSTRATION 5.11
1 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
In the following figure G, is centroid of the triangles ABC.
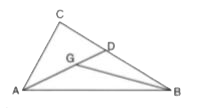
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
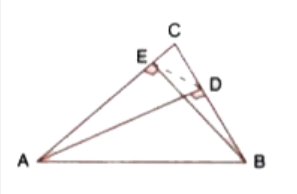
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
ΔADC~ΔBEC

View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
ΔABC~ΔDEC
View SolutionIn triangle ABC , base BC and area of triangle are fixed. The locus of the centroid of triangle ABC is a straight line that is a) parallel to side BC (b)right bisector of side BC (c)perpendicular to BC (d)inclined at an angle sin−1(√BC) to side BC
View SolutionA straight line moves in such a way that the length of the perpendicular upon it from the origin is always p. Find the locus of the centroid of the triangle which is formed by the line and the axes.
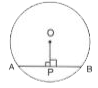
View SolutionThe following figure shows a circle with centre O.
If OP is perpendicular to AB, prove that AP = BP.
View SolutionA variable line passing through point P(2,1) meets the axes at A and B . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View SolutionP is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.
View SolutionFind the co-ordinates of the centroid of a triangle ABC whose vertices are :
A(-1, 3), B(1, -1) and C(5, 1)
View Solution
