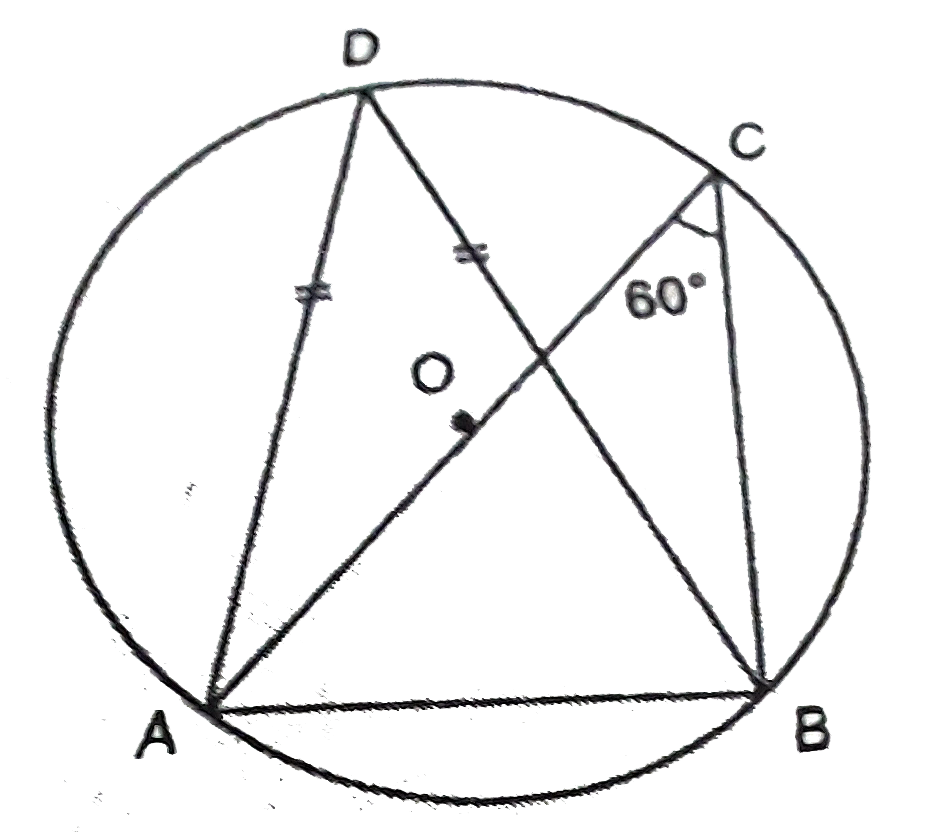
In the following figure O is the centre of the circel. If ∠ACB=60∘ and DA=DB then prove that ΔADB is an equilateral triangle.
Video Solution
Text Solution
∠ADB=∠ACB (angles of same segment)
∠ADB=60∘
⇒
In ΔADB,
AD=DB
AD=DB
⇒∠ABD=∠BAD
and ∠ABD+∠BAD+∠ADB=180∘
⇒∠ABD+∠ABD+60∘=180∘
⇒2∠ABD=120∘
⇒∠ABD=60∘
∴∠ABD=∠BAD=∠ADB=60∘
⇒ΔABD is an equilateral triangle.
|
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
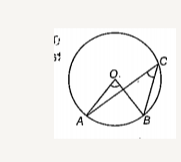 A25∘B50∘C75∘D60∘
A25∘B50∘C75∘D60∘In the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘In the given figure, O is the centre of the clrcle. ∠ABO=60∘. Find the value of ∠ACB :
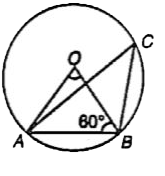 A40∘B60∘C50∘D30∘
A40∘B60∘C50∘D30∘
In the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
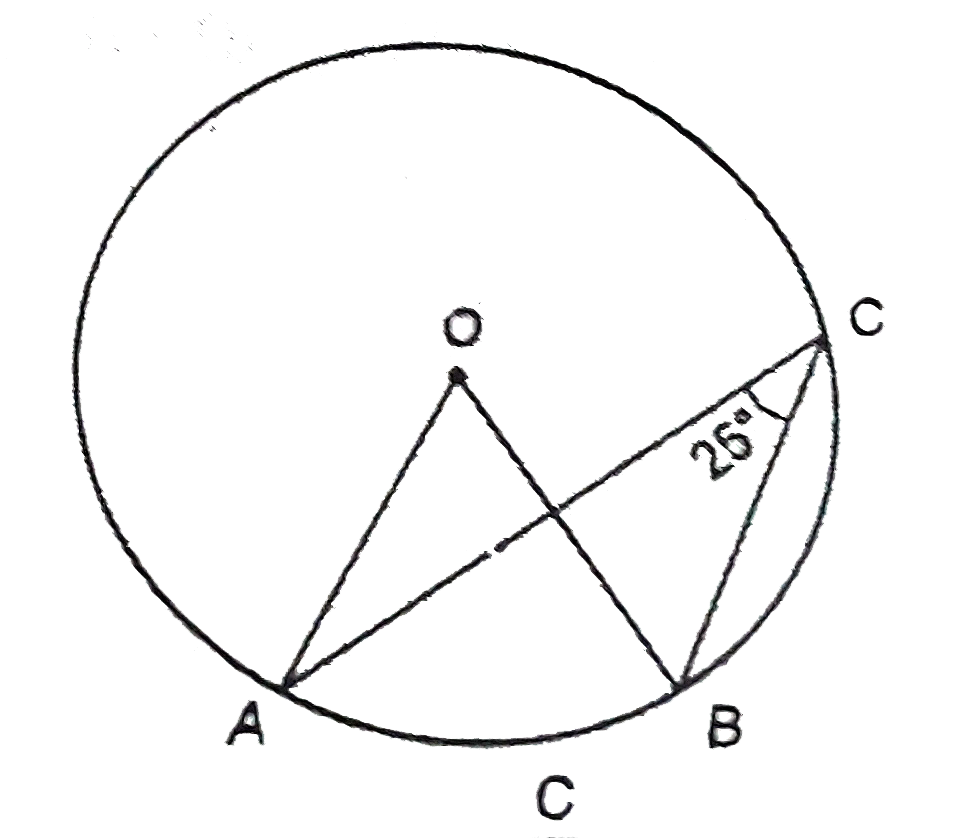
View SolutionProve that each angle of an equilateral triangle is 600
View SolutionProve that the medians of an equilateral triangle are equal.
View SolutionProve that an equilateral triangle is equiangular.
View SolutionIn the given figure, ΔABC is an equilateral triangle. Find ∠BEC :
View Solution

