In the following, shade the region, where the following inequations hold. Also find the vertices of the region so formed:
x≥2,x≤8,y≥−4,y≤x+2,2x+y≤14.
The correct Answer is:(2,4),(4,6),(9,-4) and (2,-4)
To solve the problem of shading the region defined by the given inequalities and finding the vertices of the region, we will follow these steps:
Step 1: Write down the inequalities
The inequalities given are:
1. x≥2
2. x≤8
3. y≥−4
4. y≤x+2
5. 2x+y≤14
Step 2: Graph the boundary lines
We will first convert the inequalities into equations to find the boundary lines.
1. For x=2: This is a vertical line at x=2.
2. For x=8: This is a vertical line at x=8.
3. For y=−4: This is a horizontal line at y=−4.
4. For y=x+2: This line has a y-intercept of 2 and a slope of 1.
5. For 2x+y=14: Rearranging gives y=−2x+14, which has a y-intercept of 14 and a slope of -2.
Step 3: Find the intersection points
Next, we need to find the points of intersection of the lines to determine the vertices of the region.
1. Intersection of y=x+2 and y=−4:
−4=x+2⟹x=−6(not in the region)
2. Intersection of y=x+2 and 2x+y=14:
Substitute y=x+2 into 2x+y=14:
2x+(x+2)=14⟹3x+2=14⟹3x=12⟹x=4
Substitute x=4 back into y=x+2:
y=4+2=6⇒(4,6)
3. Intersection of y=−4 and 2x+y=14:
Substitute y=−4:
2x−4=14⟹2x=18⟹x=9⇒(9,−4)
4. Intersection of y=−4 and y=x+2:
−4=x+2⟹x=−6(not in the region)
5. Intersection of y=−4 and x=2:
(2,−4)
6. Intersection of y=−4 and x=8:
(8,−4)
Step 4: Identify the vertices
The vertices of the region formed by the inequalities are:
1. (2,−4)
2. (4,6)
3. (8,−4)
4. (2,4) (from y=x+2 at x=2)
5. (9,−4) (from 2x+y=14 at y=−4)
Step 5: Shade the region
Now, we will shade the region that satisfies all the inequalities:
- The region is bounded by the lines x=2 and x=8 on the left and right.
- The region is above the line y=−4 and below the lines y=x+2 and 2x+y=14.
Final Answer
The vertices of the region are:
- (2,−4)
- (4,6)
- (8,−4)
The inequalities given are:
1. x≥2
2. x≤8
3. y≥−4
4. y≤x+2
5. 2x+y≤14
We will first convert the inequalities into equations to find the boundary lines.
2. For x=8: This is a vertical line at x=8.
3. For y=−4: This is a horizontal line at y=−4.
4. For y=x+2: This line has a y-intercept of 2 and a slope of 1.
5. For 2x+y=14: Rearranging gives y=−2x+14, which has a y-intercept of 14 and a slope of -2.
Next, we need to find the points of intersection of the lines to determine the vertices of the region.
−4=x+2⟹x=−6(not in the region)
Substitute y=x+2 into 2x+y=14:
2x+(x+2)=14⟹3x+2=14⟹3x=12⟹x=4
Substitute x=4 back into y=x+2:
y=4+2=6⇒(4,6)
Substitute y=−4:
2x−4=14⟹2x=18⟹x=9⇒(9,−4)
−4=x+2⟹x=−6(not in the region)
(2,−4)
(8,−4)
The vertices of the region formed by the inequalities are:
1. (2,−4)
2. (4,6)
3. (8,−4)
4. (2,4) (from y=x+2 at x=2)
5. (9,−4) (from 2x+y=14 at y=−4)
Now, we will shade the region that satisfies all the inequalities:
- The region is bounded by the lines x=2 and x=8 on the left and right.
- The region is above the line y=−4 and below the lines y=x+2 and 2x+y=14.
The vertices of the region are:
- (2,−4)
- (4,6)
- (8,−4)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - CHECH YOUR UNDERSTANDING10videos
LINEAR INEQUATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - CHAPTER TEST12videos
LINEAR INEQUATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - NCERT EXERCISE 6.124videos
LINEAR INEQUATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - CHECK YOUR UNDERSTANDING10videos
LIMITS AND DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL INDUCTIONEXERCISE - CHAPTER TEST 412videos
MATHEMATICAL INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following shaded regions shows the graph of the inequality y≤|x+2| ?
A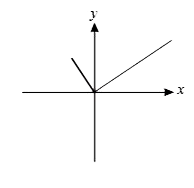 B
B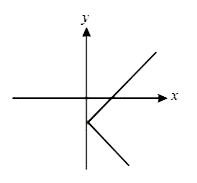 C
C D
D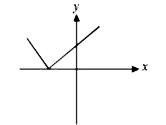
- Question 2 - Select One
The area of the region {(x,y):xy≤8,≤y≤x2} is
A8loge2−143B8loge2−73C16loge2−143D16loge2−6 - Question 3 - Select One
A vertex of bounded region of inequalities x≥0,x+2y≥0 and 2x+y≤4, is
A(1,1)B(0,1)C(3,0)D(0,0)
Find the region when the following inequations:
x+y≤6,x≥y,x≥0,y≤0 hold good. Find the coordinates of the vertices of the region.View SolutionFind the region enclosed by the following inequations:
x+y−2≤0,2x+y−3≤0,x≥0,y≥0.
Also, find the ordered pairs of the vertices of the region.View SolutionFind the region enclosed by the following inequations:
x+y−2≤0,2x+y−3≤0,x≥0,y≥0.
Also, find the ordered pairs of the vertices of the region.View SolutionFind the area of the region {x,y:x2+y2≤2ax,y2≥ax,x≥0,y≥0}
View SolutionThe area of the region satisfying x≤2,y≤|x|andx≥0 is
View Solution

