In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
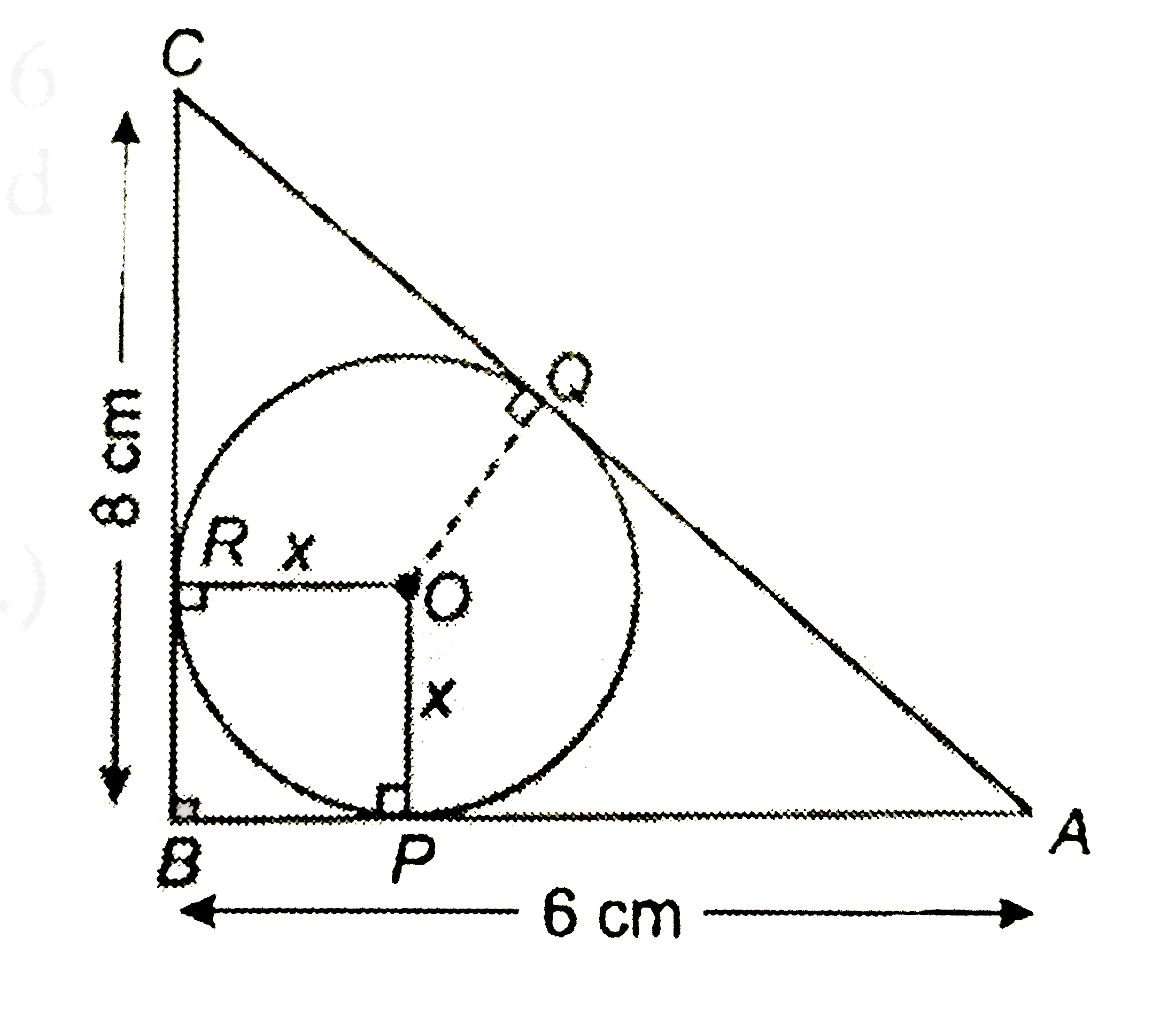
Let x be the radius of the circle. In right triangle ABC,
AC2=AB2+BC2 (by Pythagoras Th.)
⇒ AC2=62+82
⇒ AC2=36+64
⇒ AC2=100
⇒ AC=10
Now in quadrilateral OPBR
∠B=∠P=∠R=90∘ each
Hance, ∠ROP=90∘ (sum of all angles of a quadrilateral is 360^(@))
and also OP=OR (each radii)
Hence, OPBR is a square with each side x cm.
Hence, BP=RB=xcm
Therefore, CR=(8-x) and PA=(6-x)
Since, the tangents from an external point to a circle are equal in length
∴AQ=AP=(6−X)andCQ=CR=(8−x)
Now, AC=AQ+CQ
⇒ 10=6−x+8x
⇒ 10=14−2x
⇒ x=2cm
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
9 Videos
Similar Questions
In the given figure ΔABC is right angle at A with AB=6 cm and AC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of r, the radius of the inscribed circle.
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View Solution
Knowledge Check
ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cmΔABC is right angled triangled with AB=6 cm, BC=8cm. O is the in centre of the triangle.The ratius of the in -circle is :
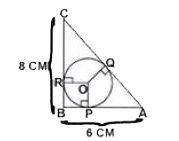 A2cmB5cmC4cmD3cm
A2cmB5cmC4cmD3cm
PQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
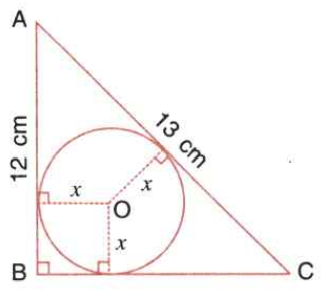
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionΔABC is a right angled triangle with ∠A=900AB=bcm,AC=acm,andBC=ccmAcircle is inscribed in this triangle. The radius of the circle,in cm, is:
View SolutionIn triangle ABC,right angled at B, BC = 24 cm, and AB = 7 cm. A circle is inscribed in triangle ABC. Then the radius of the circle is:
View SolutionIn the given figure,ABC is a right angled triangle in which ∠A=90∘,AB=21 cm and AC=28 cm.Semi-circles are drawn on AB, BC and AC as diameters. Find the area of shaded region.
View SolutionABC is a right angled triangle, right angled at B such that BC=6cm and AB=8cm . A circle with centre O is inscribed in ABC . The radius of the circle is (a) 1cm (b) 2cm (c) 3cm (d) 4cm
View Solution
