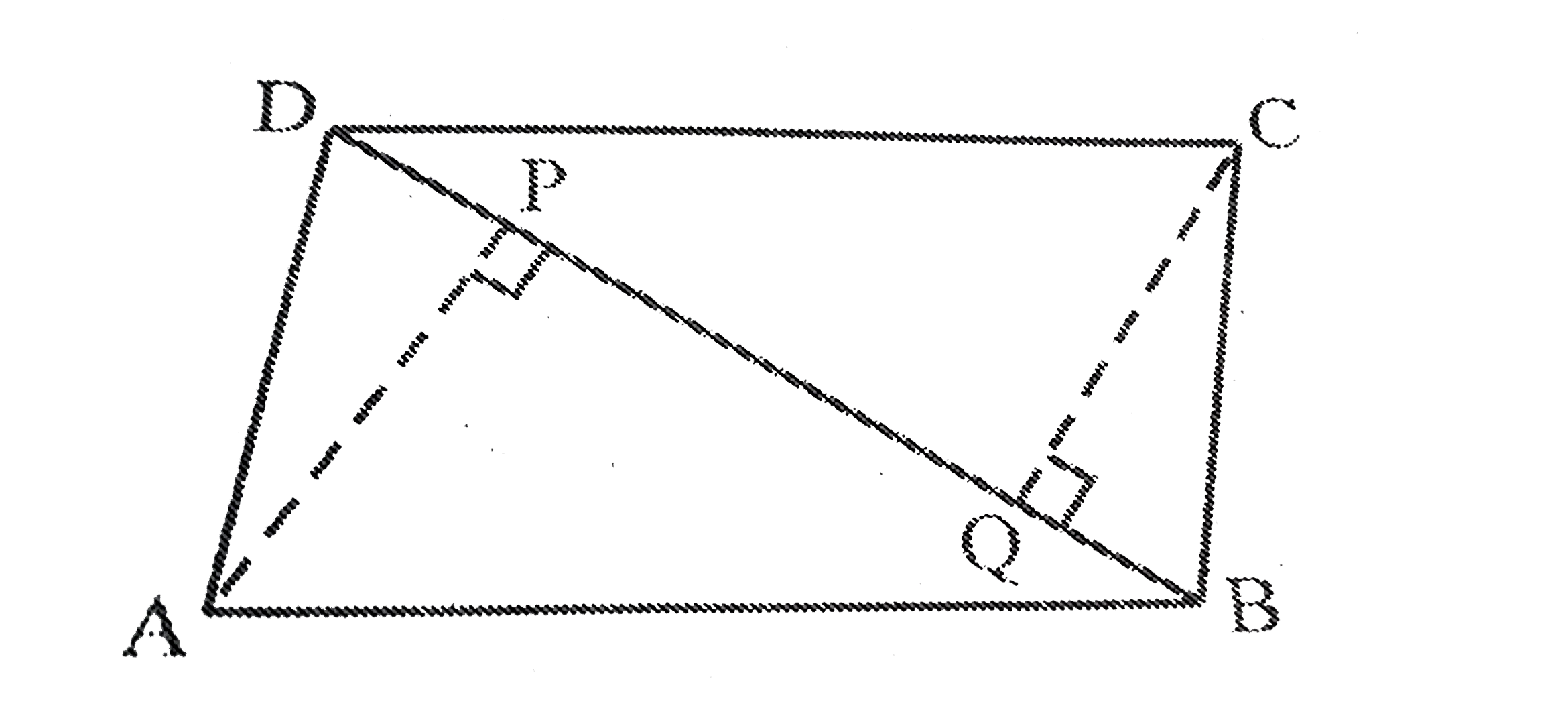
In the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
Video Solution
Text Solution
(i)InΔADNandΔCBP
∵⎧⎪⎨⎪⎩∠AND=∠CBP(each90∘)AD=CB(opposite sides of a parallelogram)∠ADN=∠CVBP(alternate anglesAD∣∣BC
∴ ΔADH≅ΔCBP (AAS theorem)
(ii)∵ ΔADN≅ΔCBP
∴ AN∣CP (c.p.c.t)
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
Knowledge Check
ABCD is a quadrlateral in which BD and AC are diagonals then
AAB+BC+CD+AD<AC+BDBAB+BC+CD+DA>AC+BDCAB+BC+CD+DA=AC+BDDAB+BC+CD+DA>2(AC+BD)ABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
A4A→BB3A→BC2A→BDA→B
The given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN. Prove that:
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
diagonal AC = diagonal BD

View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.
View SolutionIf AM and CN are perpendiculars on the diagonal BD of a parallelogram ABCD, Is ΔAMD≅ΔCNB? Give reason.
View Solution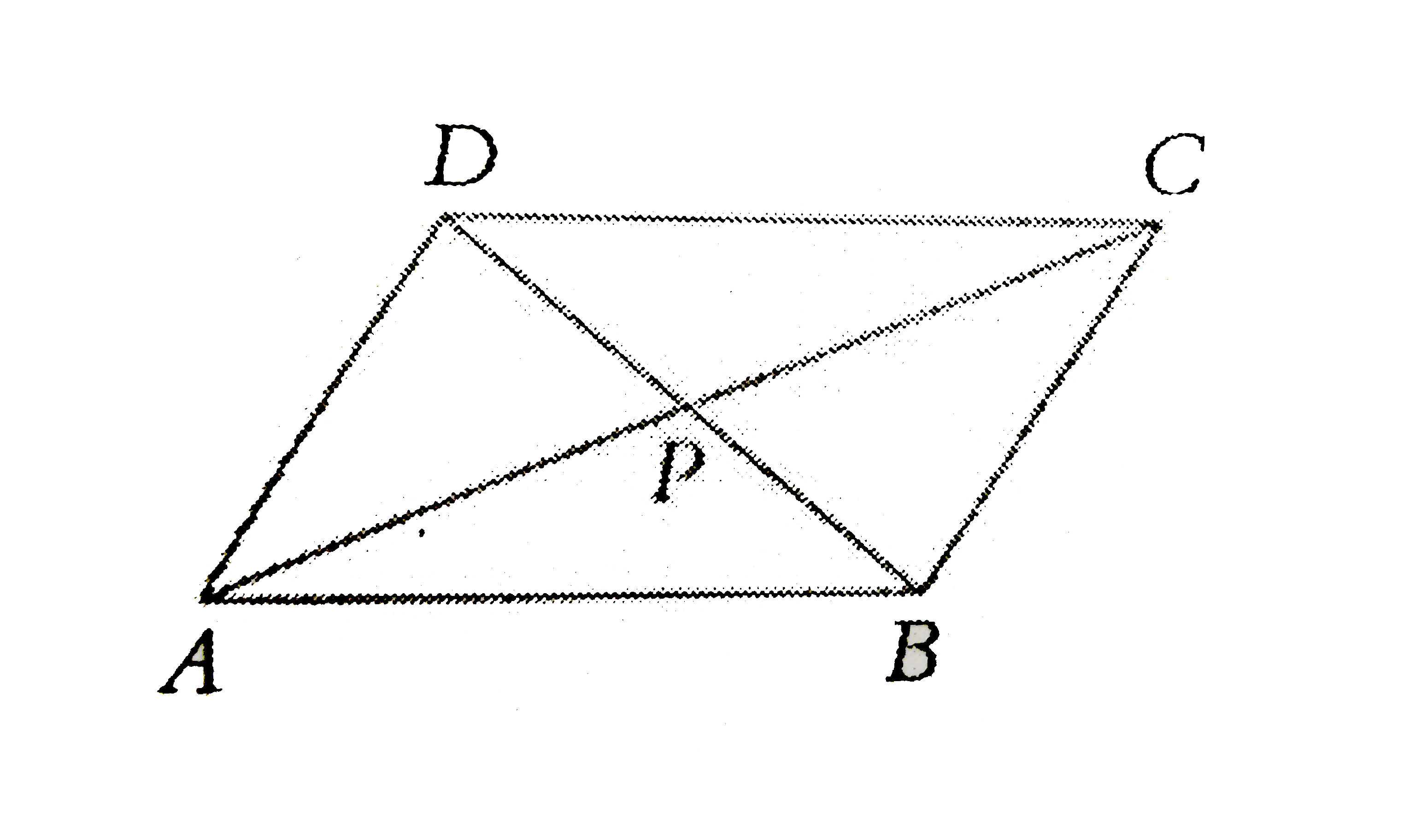
In the figure above, ABCD is a parallelogram , and if AC=30 cm and BD=20 cm, find CP+DP.
View SolutionIn the figure ABCD and DXBY are two parallelograms with BD as the common diagonal. Prove that AYCX is also a parallelogram.
View Solution