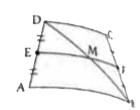
In the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that $E F = \frac{1}{2} (A B + D C)$ .

Video Solution

Text Solution

Verified by Experts

Join AC which interests EF at G.
In $△ A D C, E G || D C$
and E is the mid-point of AD
then G is mid-point of AC (converse of mid-point theorem)
Again, E is mid point of AD.
Since, G is mid-point of AC,
$E G = \frac{1}{2} D C$ (mid point theorem)...(1)
Now, EF"||" AB
EF"||"AB
In $△ C A D,$
Since, G is mid-point of CA,
and $G F || A B (b e c u a s e E F || A B)$
$∴$ F is mid point of CB. (converse of mid-point theorem)
In $△ C A B$ ,
Since, F is mid point of CB.
and G is mid-point of CA.
$∴ G F = \frac{1}{2} A B$ (mid-point theorem)...(2)
Adding (1) and (2), we get
$E G + G F = \frac{1}{2} (C D + A B)$
$\Rightarrow E F = \frac{1}{2} (A B + C D)$ Hence proved.