In the given figure, FD is the bisector of ∠EFG, also ∠FDE=∠FDG. Prove that △DFE≅△DFG,DE=DG and ∠FED=∠FGD.

Step by step video & image solution for In the given figure, FD is the bisector of angleEFG, also angleFDE = angleFDG. Prove that triangleDFE ~= triangleDFG, DE = DG and angleFED = angleFGD. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure AB⊥BEandEF⊥BE. Also BC=DE and AB= EF. Then
 AΔABD≅ΔEFCBΔABD≅ΔEFCCΔABD≅ΔCMDDΔABD≅ΔCEF
AΔABD≅ΔEFCBΔABD≅ΔEFCCΔABD≅ΔCMDDΔABD≅ΔCEF
In the given figure, DE || QR and AP and BP are bisectors of ∠EABand∠RBA, respectively. The value of ∠APB=

View SolutionIn the given figure, ray AE ∣∣ ray BD, ray AF is the bisector of ∠EAB and ray BC is the bisector of ∠ABD . Prove that lineAF ∣∣ line BC.

View SolutionIn the figure given below PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.

View SolutionIn the given figure, if line AB ∣∣ line CF and line BC ∣∣ line ED, then prove that ∠ABC=∠FDE .

View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
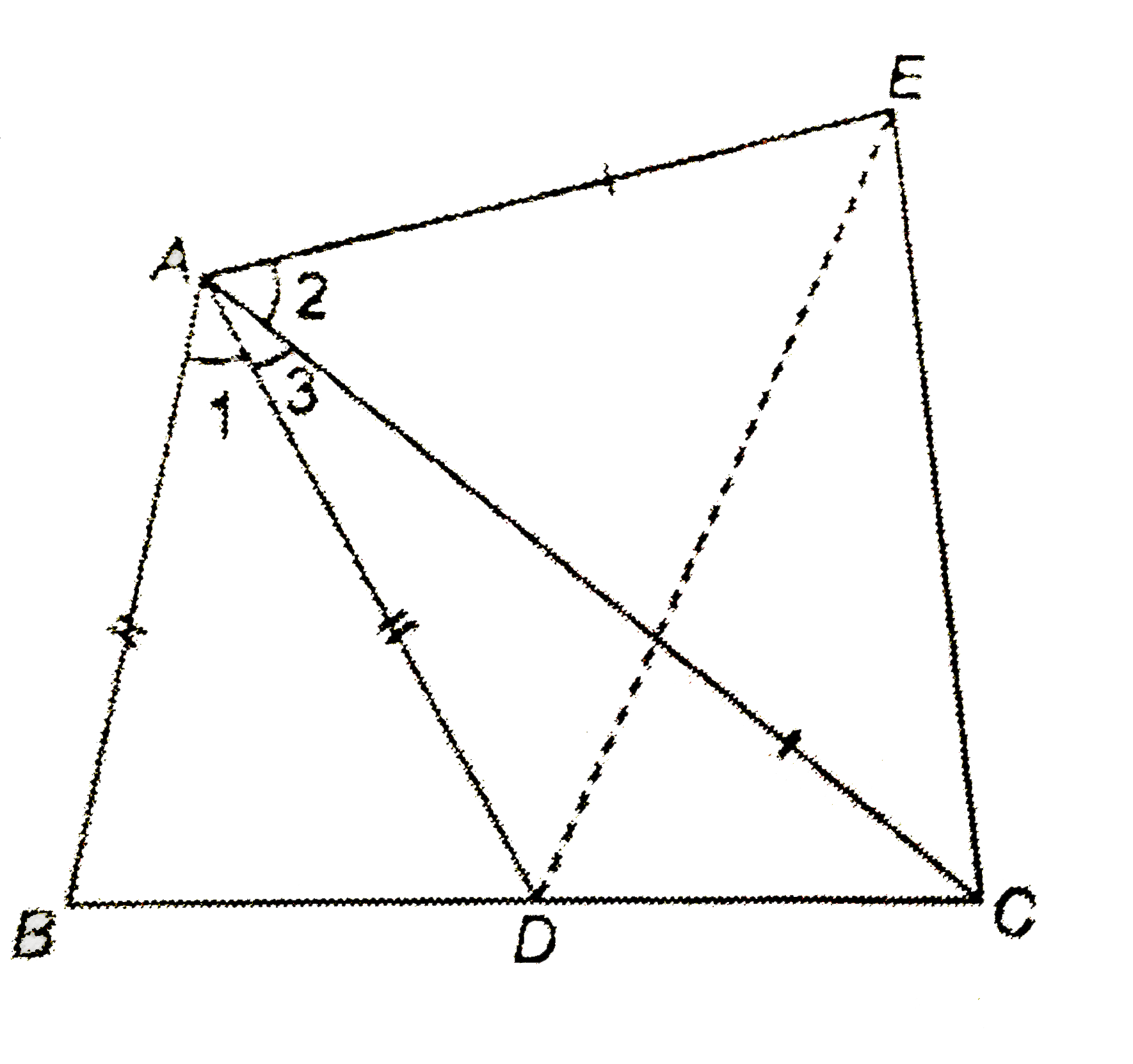
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
View Solution