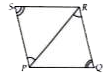
In the given figure , if ∠PQR=∠PRQ then prove that ∠PQS=∠PRT.
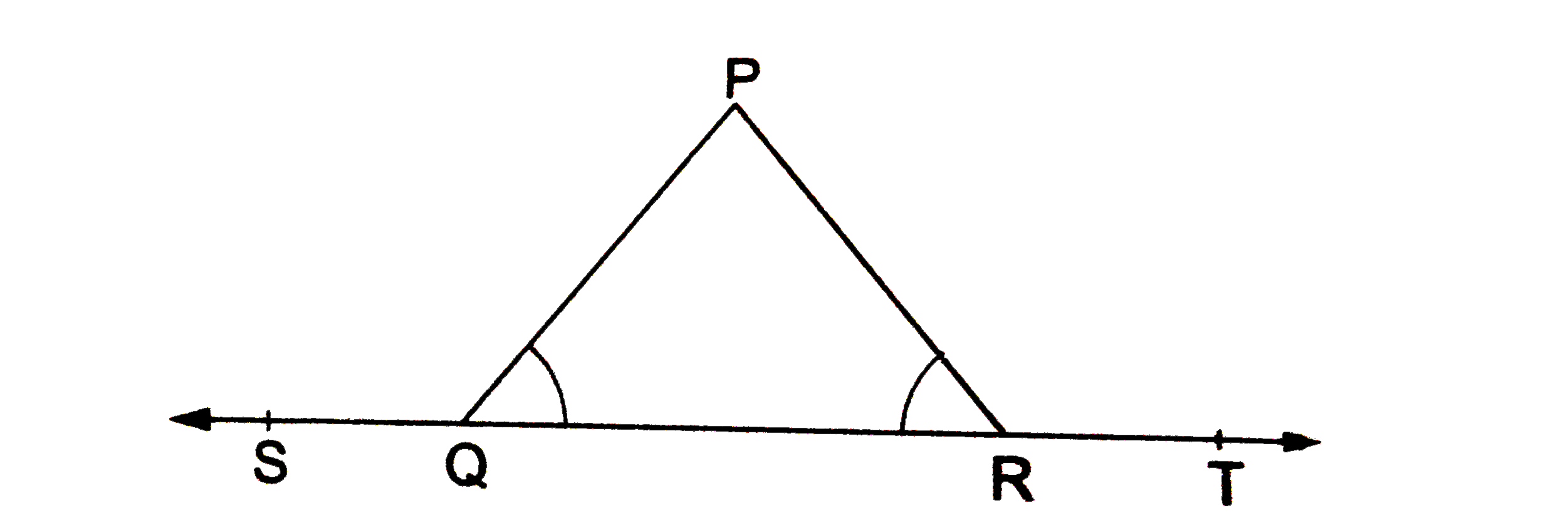
Since ray QP stands on line ST, we have
∠PQR+∠PQS=180∘. ...(i)
Again, ray RP stands on line ST.
∴∠PRQ+∠PRT=180∘. ...(ii)
From (i) and (ii), we get
∠PQR+∠PQS=∠PRQ+∠PRT
⇒∠PRQ+∠PQS=∠PRQ+∠PRT [∵∠PQR=∠PRQ]
⇒∠PQS=∠PRT.
Hence, ∠PQS=∠PRT.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example13videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A12videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)24videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)18videos
MEAN , MEDIAN AND MODE OF UNGROUPED DATA
Similar Questions
In the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
 View Solution
View SolutionIn the given figure, we have PQ = SR and Pr = SQ. Prove that:

∠PQR=∠SRQView SolutionIn the given figure below, if AC = BD then prove that AB = CD.
 View Solution
View SolutionIn the given figure, if x+y=z+w then prove that AOB is a line.
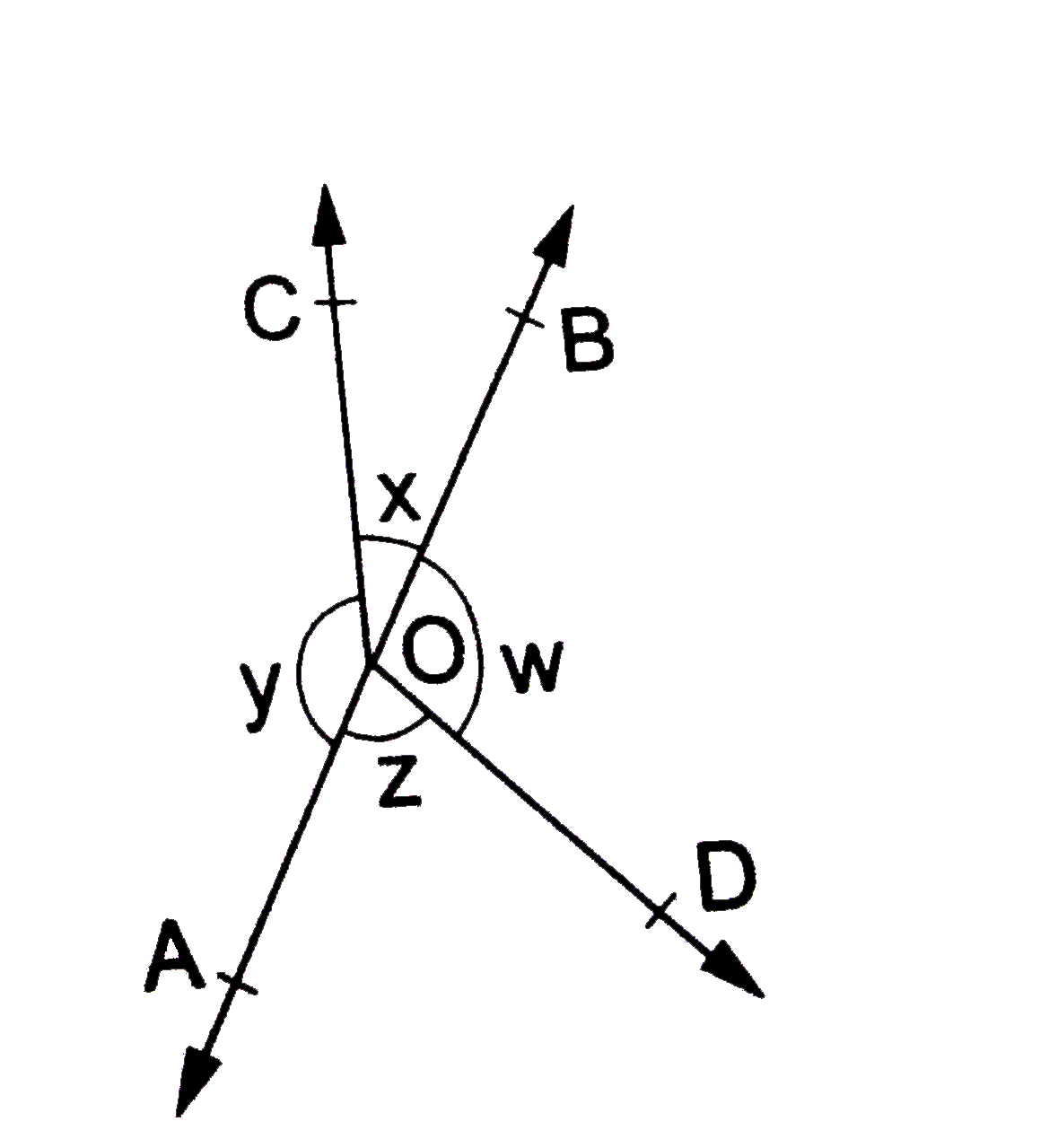 View Solution
View SolutionIn the given figure △AOB~△DOC, prove that AB||CD.
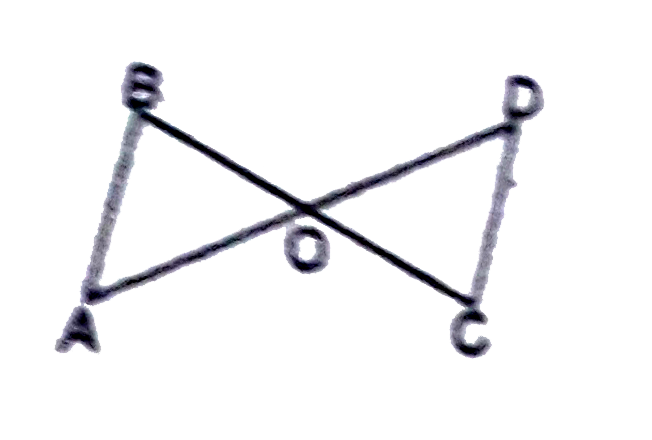 View Solution
View SolutionIn the given figure, if AC = BD, then prove that AB = CD.
 View Solution
View SolutionIn the given figure, ∠SPR=∠QRPand∠RSP=∠PQR. Prove that PQ = RS.
 View Solution
View SolutionIn the given figure PSSQ=PTTRand∠PST=∠PRQ. Prove that PQR is an isoscles triangle.
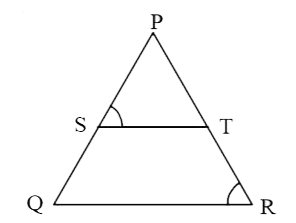 View Solution
View SolutionIn the given figure, if x=y and AB=CB, then prove that AE=CD.
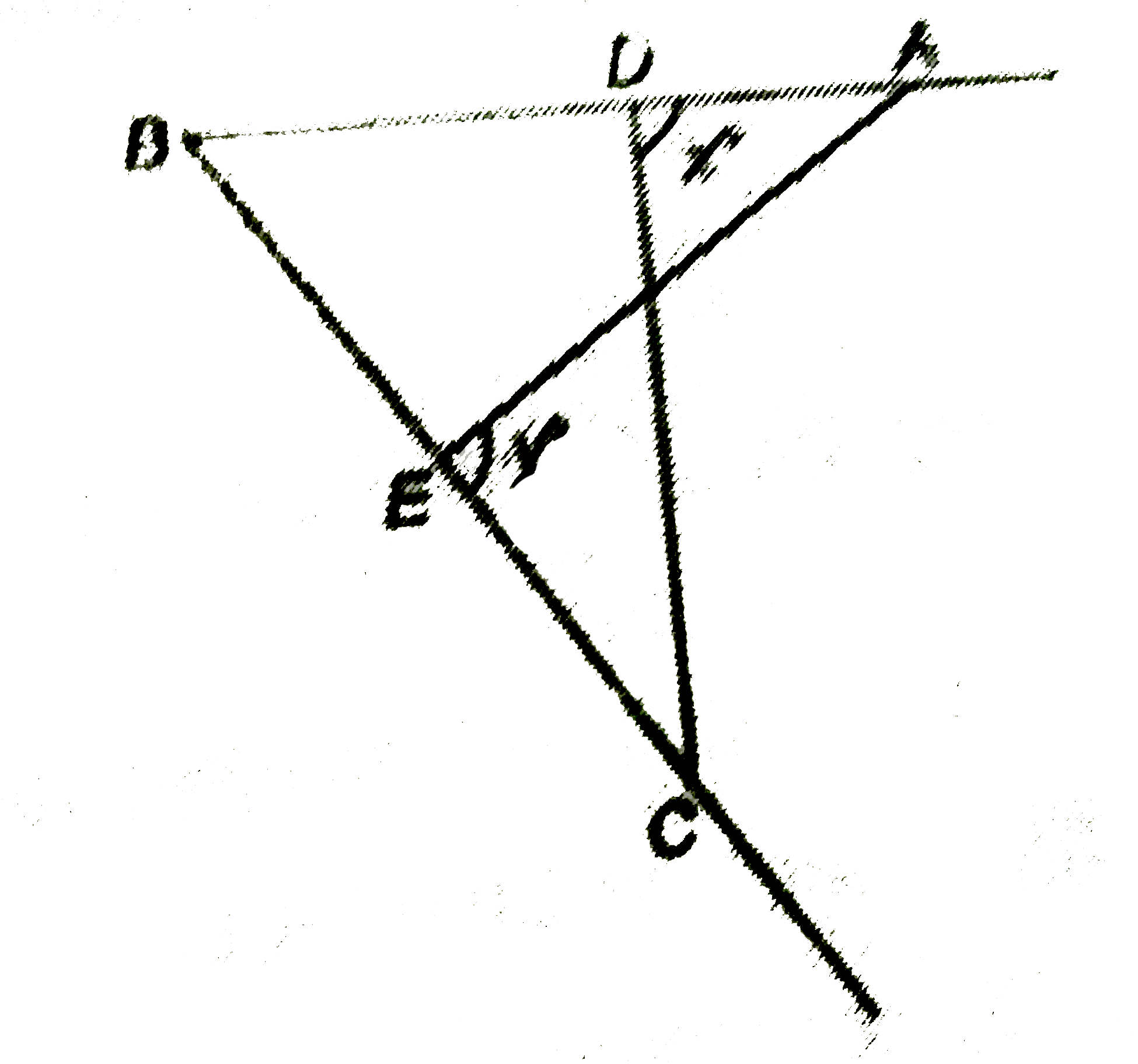 View Solution
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.
 View Solution
View Solution

