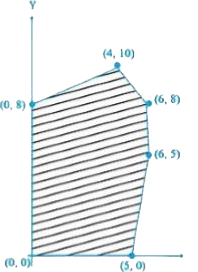
In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
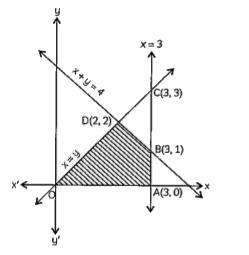
O
B
C
D
The correct Answer is:D
Step by step video, text & image solution for In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - Section - B
20 Videos
- SAMPLE PAPER 3BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3EXERCISE - Section - C
7 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - Mathematics (Section - A)
1 Videos
- SAMPLE PAPER 4 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4 EXERCISE - SECTION - C
7 Videos
Similar Questions
The feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R2 is the feasible region and the objective function is Z2=4x+3y, then the minimum value of Z2 occurs at:

View SolutionIn the given figure, the area of shaded region is ________ .

View Solution
Knowledge Check
The feasible regions for two LPP is show in the following figure.
Based on the given information, answer the following questions:
If R1 is the feasible region, and the ojective function is Z1=2x−y, then the maximum value of Z1 occurs at:
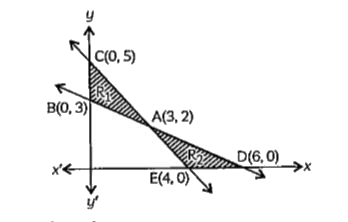 A(0,5)B(0,3)C(3,2)D(6,0)
A(0,5)B(0,3)C(3,2)D(6,0)The shaded region in the given figure is
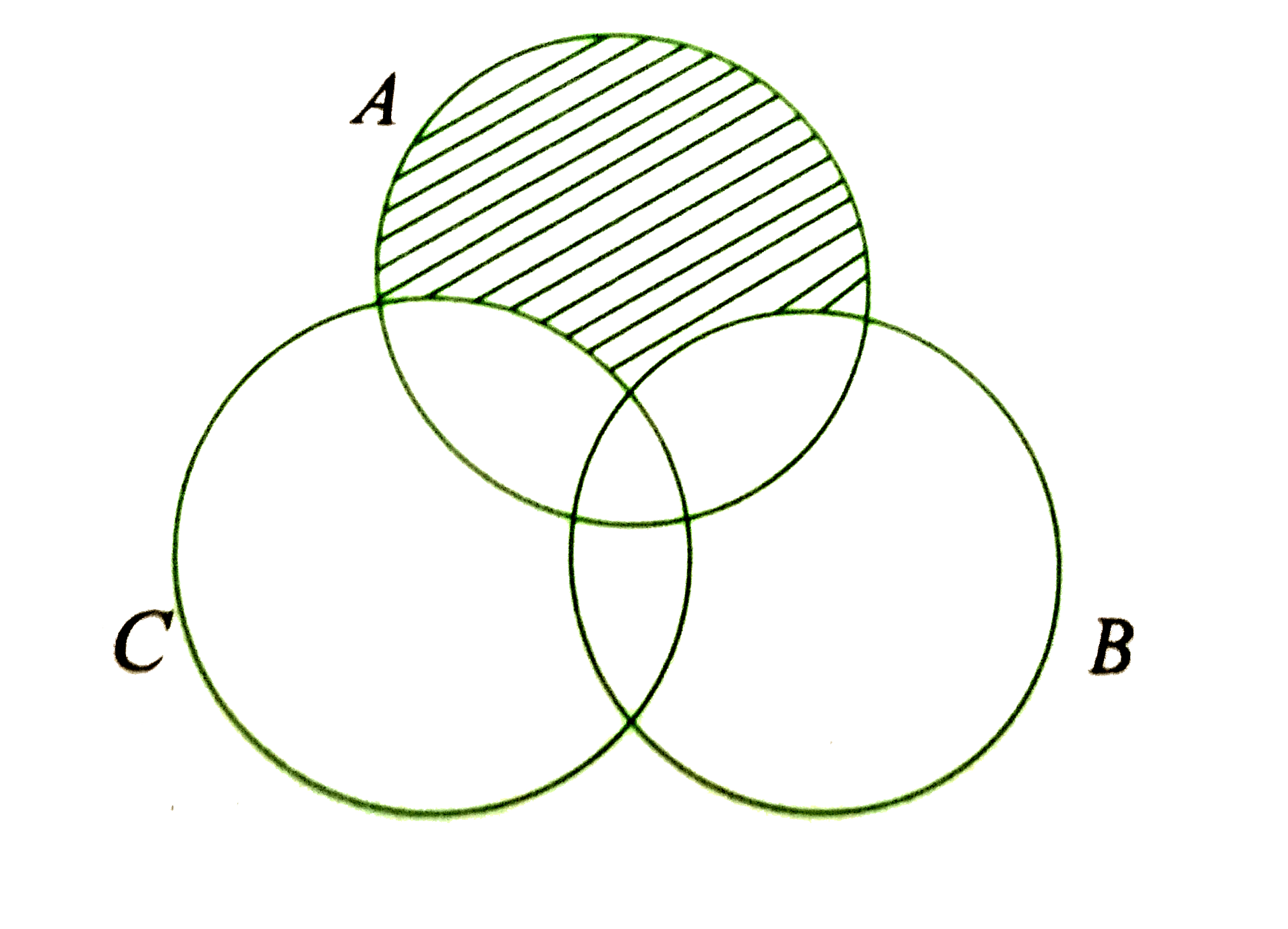 AA∩(B∪C)BA∪(B∩C)CA∩(B−C)DA−(B∪C)
AA∩(B∪C)BA∪(B∩C)CA∩(B−C)DA−(B∪C)The shaded region in the given figure is
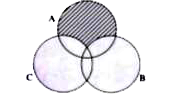 AA∩(B∪C)BA∪(B∩C)CA∩(B−C)DA−(B∪C)
AA∩(B∪C)BA∪(B∩C)CA∩(B−C)DA−(B∪C)
area of the shaded region in given figure ?
View Solution
In the given figure, what is the area of the shaded region ?
View SolutionIn the given figure,MN=x and LN=x2. What is the area of the shaded region?

View SolutionIn the given graph, the feasible region for a LPP is shaded.
The objective function Z = 2x – 3y, will be minimum at:
View SolutionThe shaded region in the given figure is

View Solution
