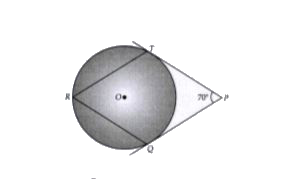
In the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
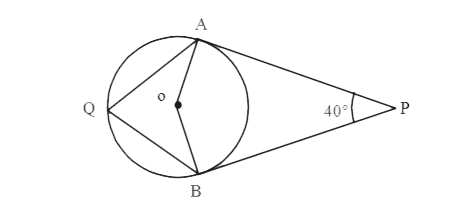
The correct Answer is:70∘
Step by step video, text & image solution for In the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find angle AQB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - SHORT ANSWER TYPE - I QUESTIONS10videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - SHORT ANSWER TYPE - II QUESTIONS4videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)1videos
ARITHMETIC PROGRESSION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D1videos
Co-ordinate Geometry
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
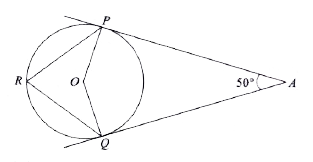 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘ - Question 2 - Select One
In the given figure , O is centre of the circle and AP = PB then APBQ is
 ArectangleBkiteCsquareDrhombus
ArectangleBkiteCsquareDrhombus - Question 3 - Select One
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
ARectangleBSquareCCyclicDNone of these
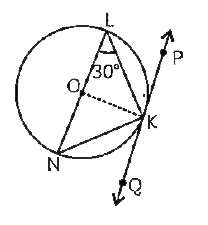
In given figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
 View Solution
View SolutionIn the figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN=30∘, find ∠PKL.
 View Solution
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
 View Solution
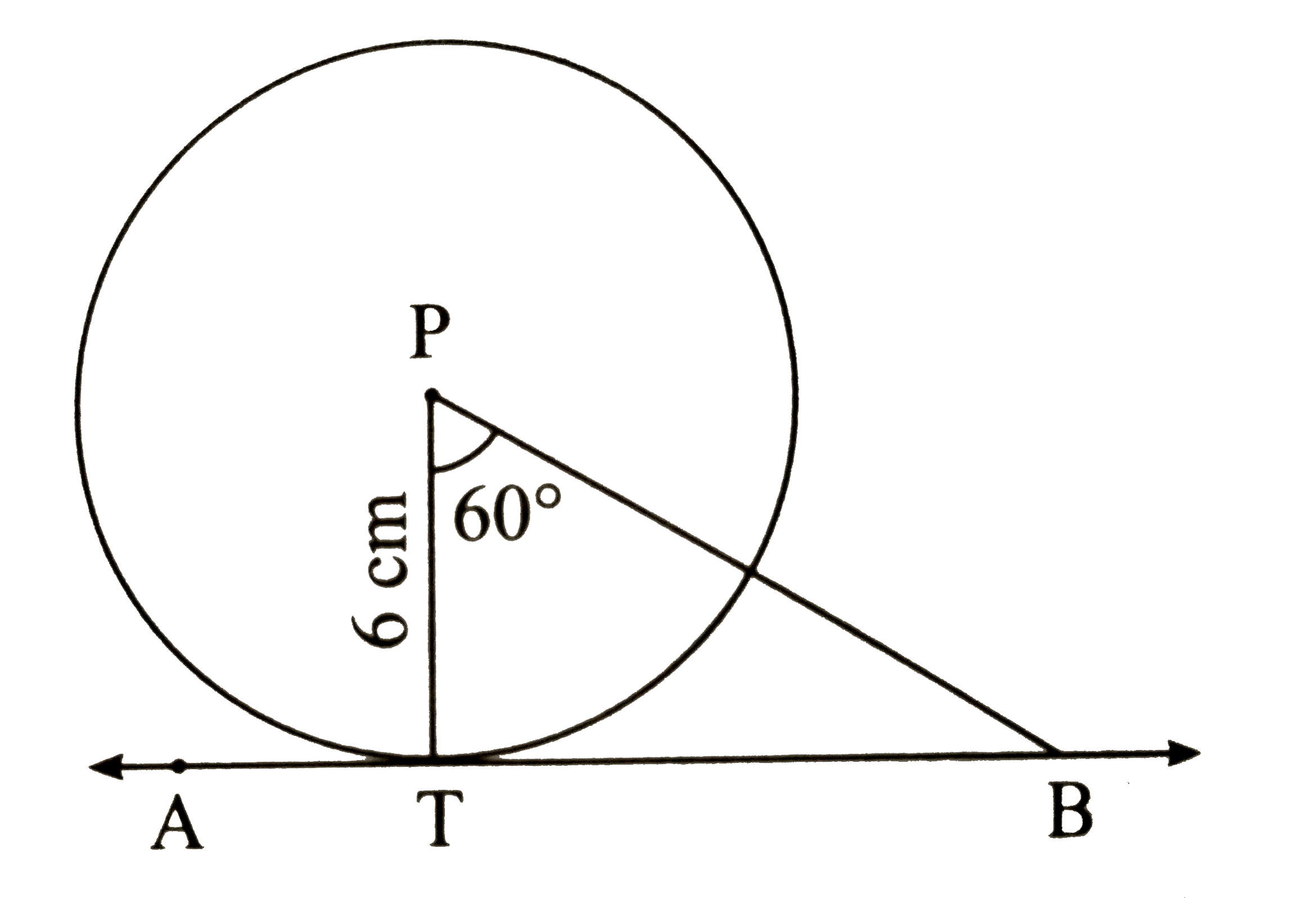
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
 View Solution
View SolutionIn the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD
 View Solution
View Solution