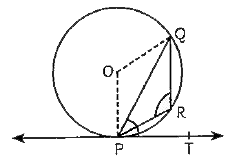
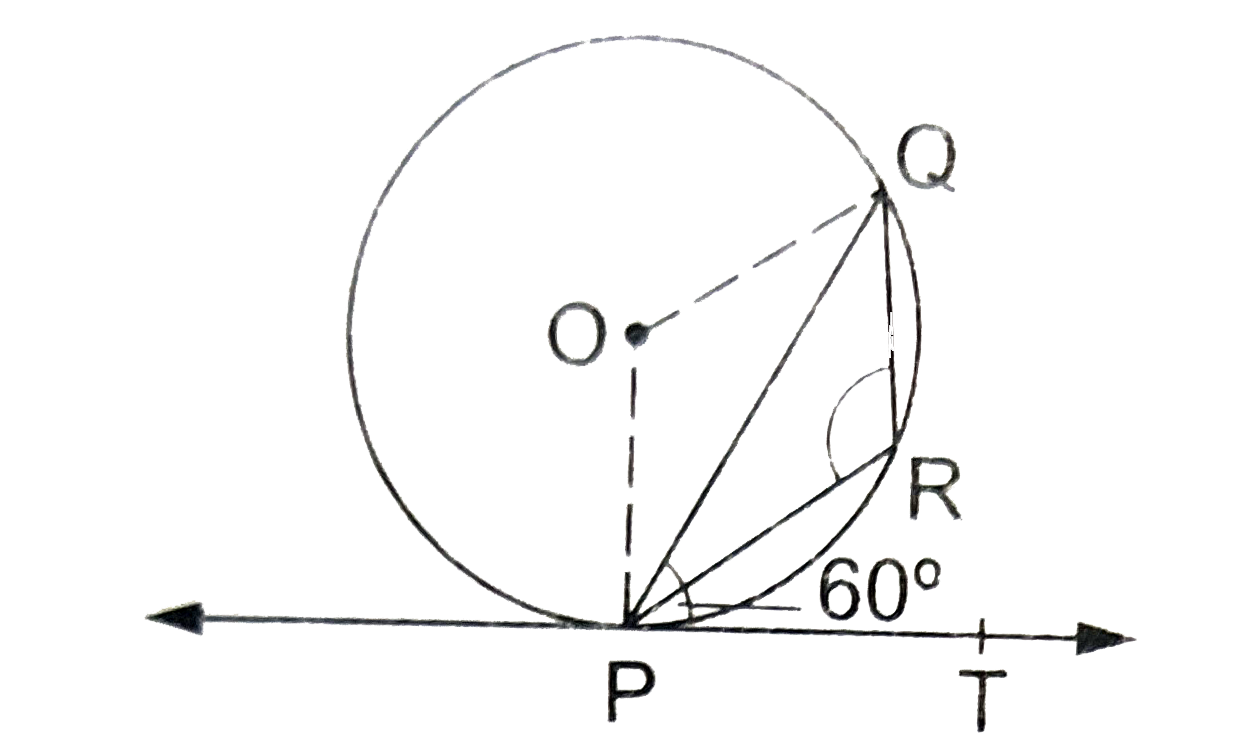
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘, find ∠PRQ.
Video Solution
Text Solution
Mark a point M in the alternate segment.
Join MP and MQ.
Then, ∠PMQ=∠QPT=60∘ [angles in the alternate segments]
Now, ∠PMQ+∠PRQ=180∘ [∵PMQR is cyclic quadrilateral]
⇒∠PRQ=180∘−∠PMQ=180∘−60∘=120∘.
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple-choice questions (MCQ)
39 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
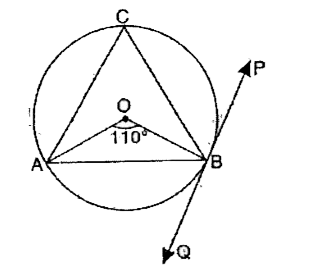 A45∘B70∘C55∘D35∘
A45∘B70∘C55∘D35∘In the figure , PQ is a chord of a circle and PT is a tangent at P such that ∠QPT=60∘, then ∠PRQ =
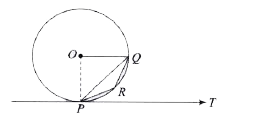 A100∘B110∘C120∘D150∘
A100∘B110∘C120∘D150∘In the given figure, O is the centre of a circle , AB is a chord and AT is the tangent at A. If ∠AOB=100∘ then ∠BAT is equal to
A40∘B50∘C90∘D100∘
In the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
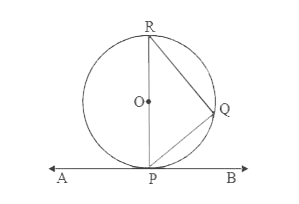
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
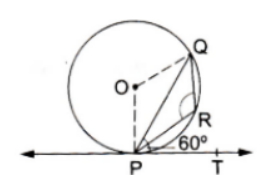
View SolutionIn the given figure, AB is a tangent to a circle with centre. Prove that ∠BPQ=∠PRQ If ∠BPQ=60∘, find ∠RPQ.
View SolutionIn the given figure, PQ is tangent at a point R of the circle with centre O. If , find m∠PRS.
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
View Solution