In the given figure, ray OC is the bisector of ∠AOB and OD is the ray opposite to OC. Show that ∠AOD=∠BOD.

Since OC is the bisector of ∠AOB,
we have
∠BOC=∠AOC. ...(i)
Since ray OB stands on line DOC at a point O, we have
∠BOC+∠BOD=180∘ ...(ii)
Again, ray OA stands on line DOC at a point O, so we have
∠AOC+∠AOD=180∘ ...(iii)
From (ii) and (iii), we get
∠AOC+∠AOD=∠BOC+∠BOD
⇒∠AOD=∠BOD [∵∠AOC=∠BOC from (i)].
Hence, ∠AOD=∠BOD.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example13videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A12videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)24videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)18videos
MEAN , MEDIAN AND MODE OF UNGROUPED DATA
Similar Questions
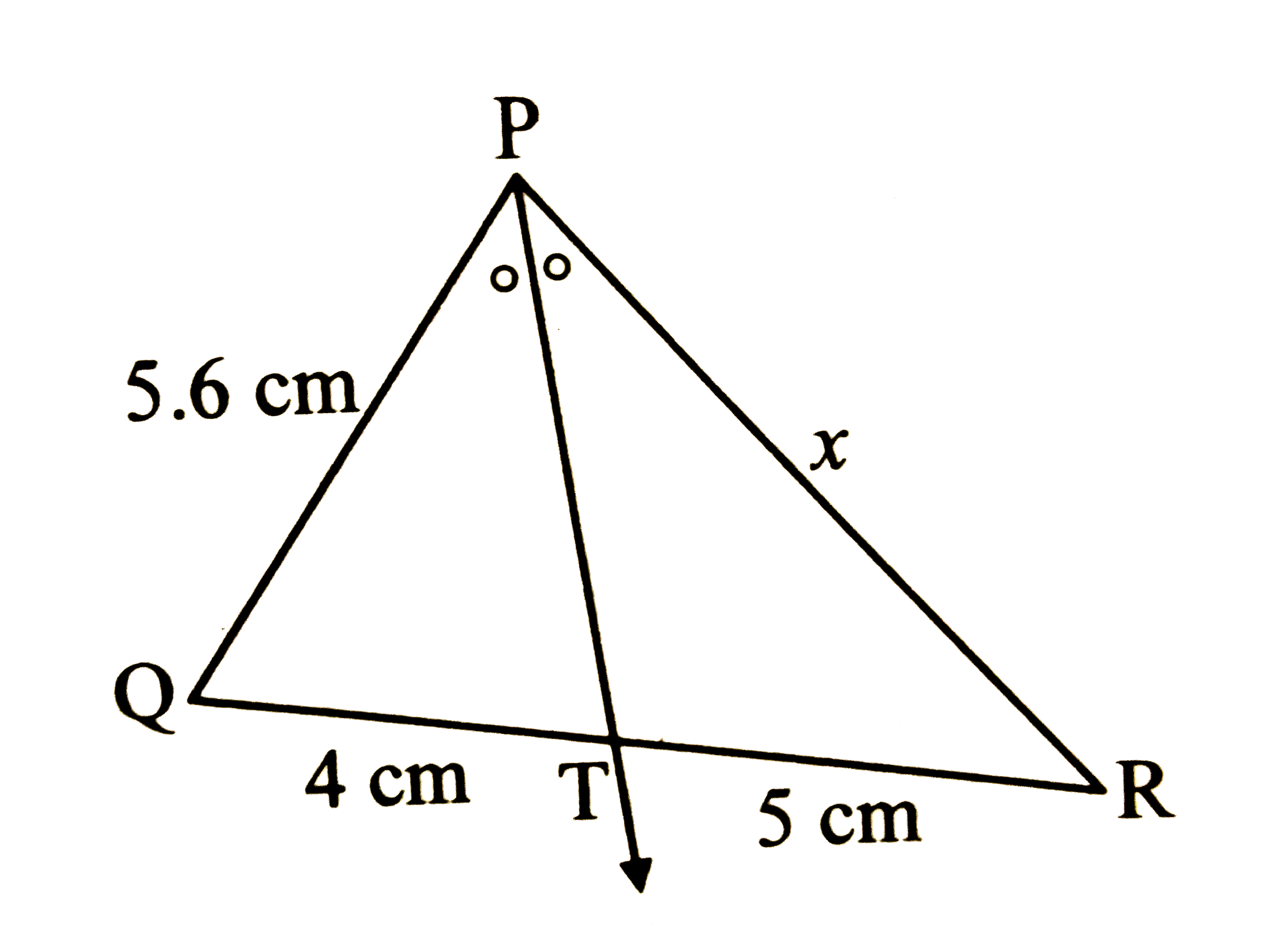
In the given figure, ray PT is the bisector of ∠QPR.
Find the value of x.
 View Solution
View SolutionIn Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
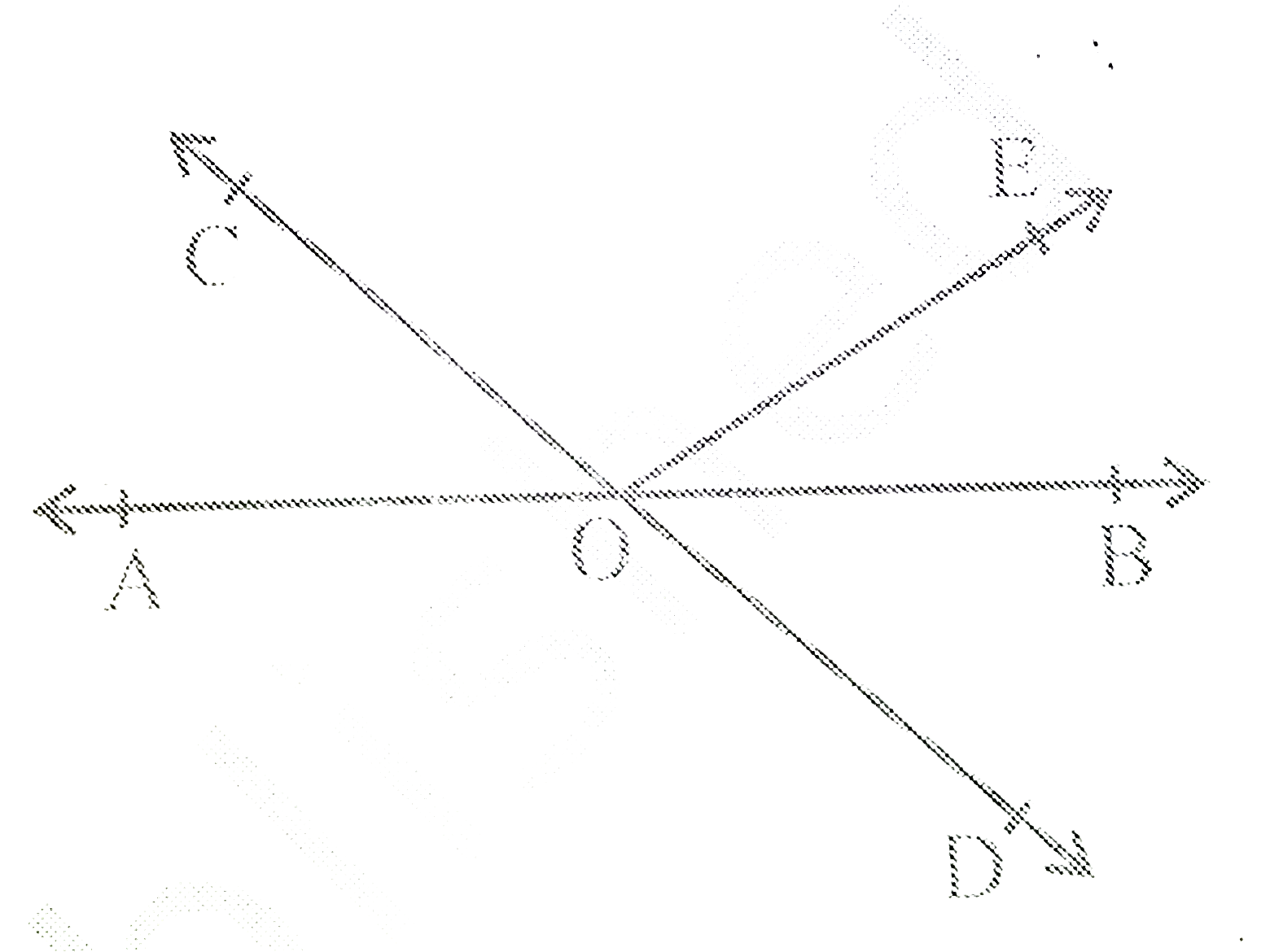 View Solution
View SolutionIn the given figure, name:

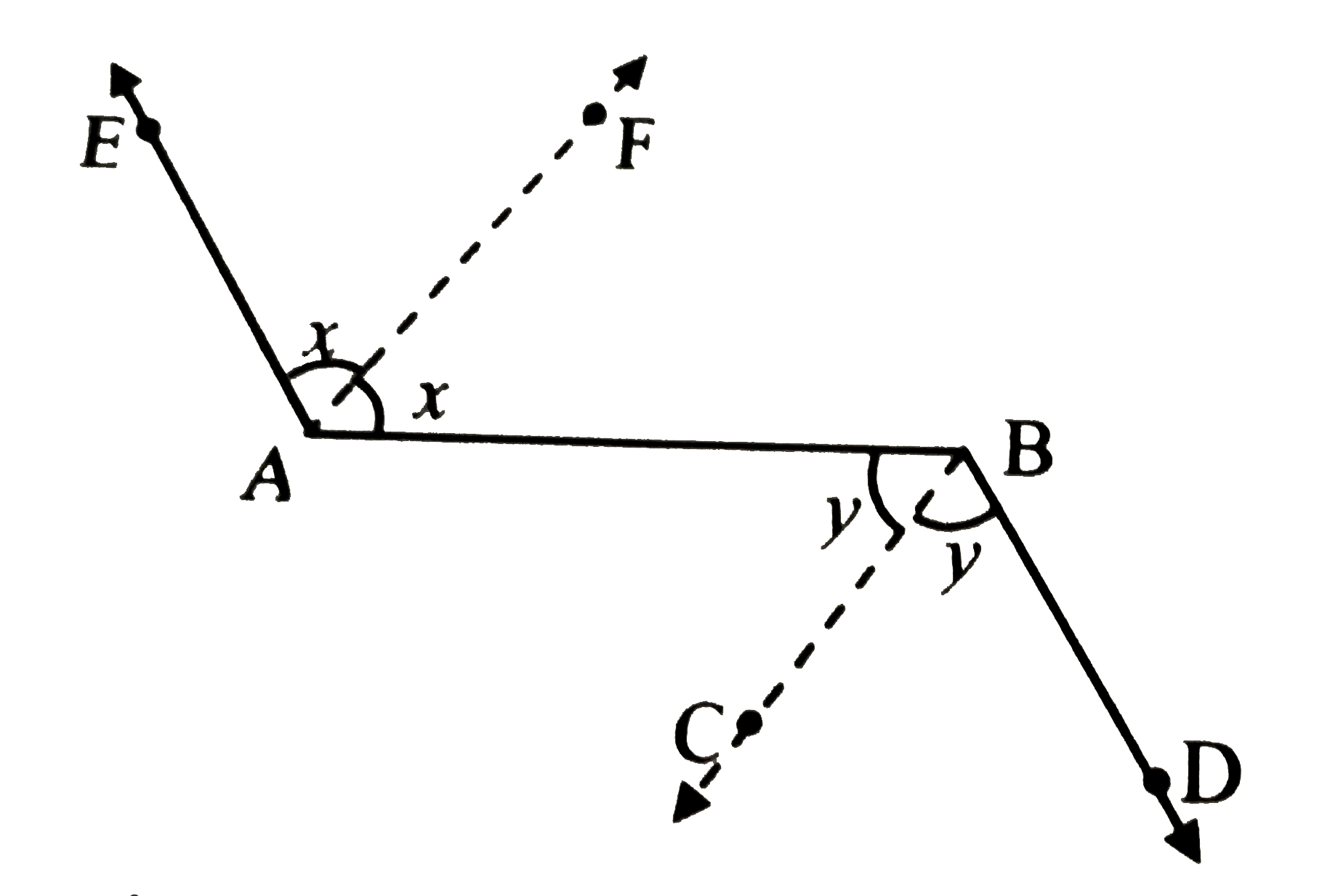
four raysView SolutionIn the given figure, ray AE ∣∣ ray BD, ray AF is the bisector of ∠EAB and ray BC is the bisector of ∠ABD . Prove that lineAF ∣∣ line BC.
 View Solution
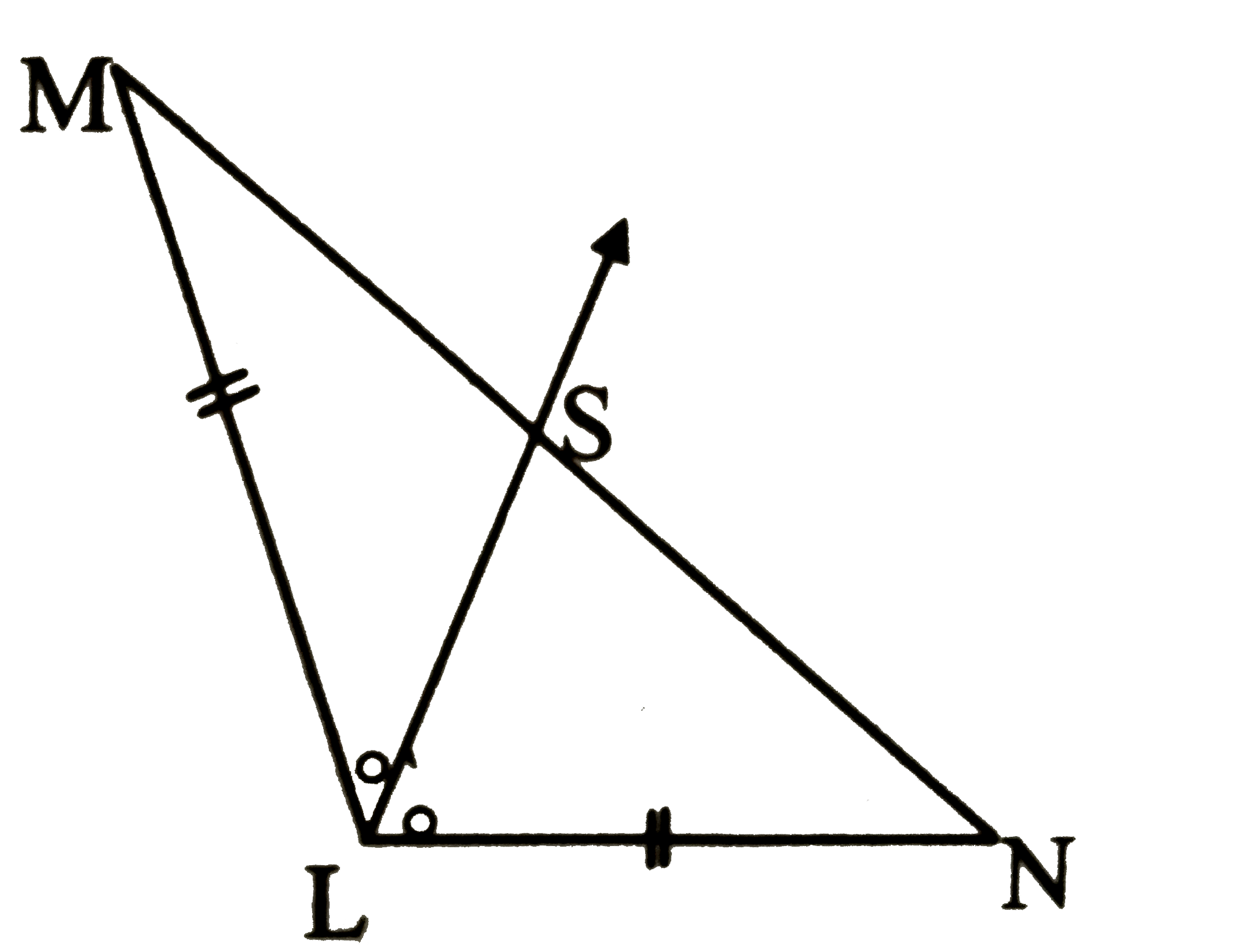
View SolutionIn the given figure, ray LS is the bisector of ∠MLN, and ML=LN. Find the relation between MS and SN.
 View Solution
View SolutionIn the figure ray QS is the bisector of ∠PQR and PQ=QR, then PSSR=………..
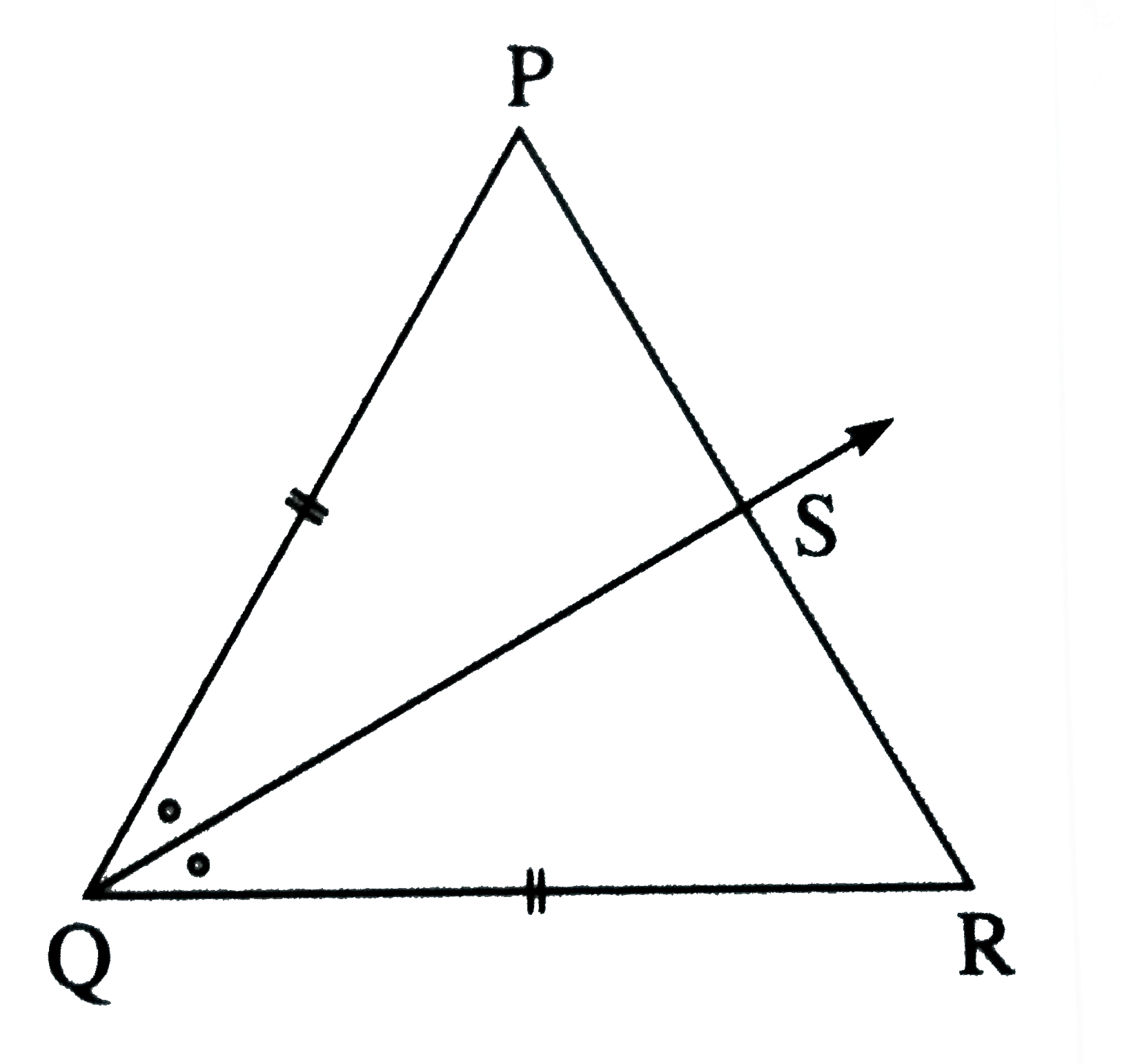 View Solution
View SolutionIn the figure, ray QS is the bisector of ∠PQR and PQ=QR.
Then PSSR=………..
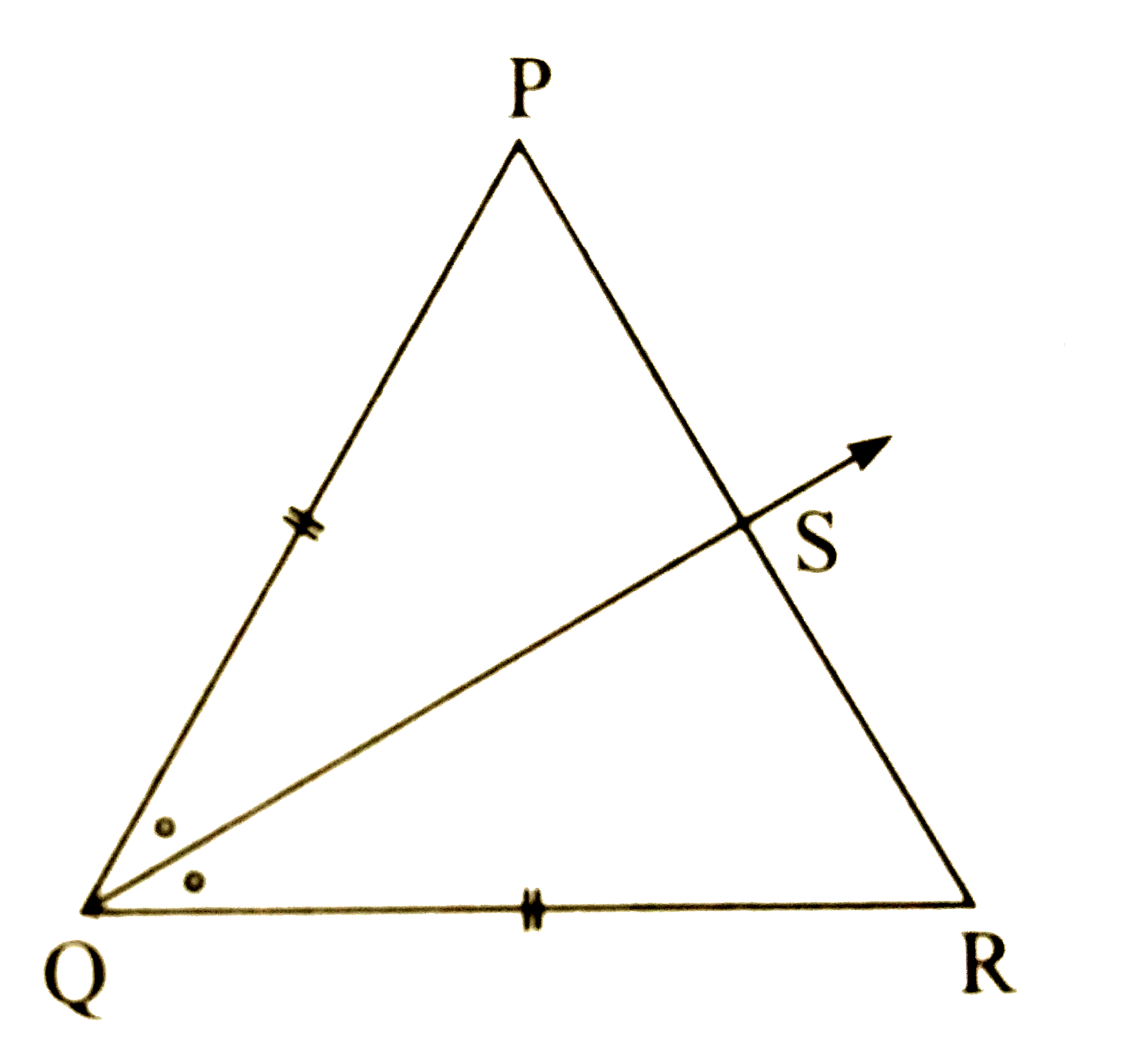 View Solution
View SolutionRay AX is the bisector of ∠BAC and ray AY is the bisector of ∠XAC. If ∠BAY=60∘, find ∠BAC.
View SolutionIn the given figure, ray OC stands on a straight line AOB. Ray OD and ray OE are the bisectors of ∠AOC and ∠BOC respectively. Find the measure of ∠DOE.
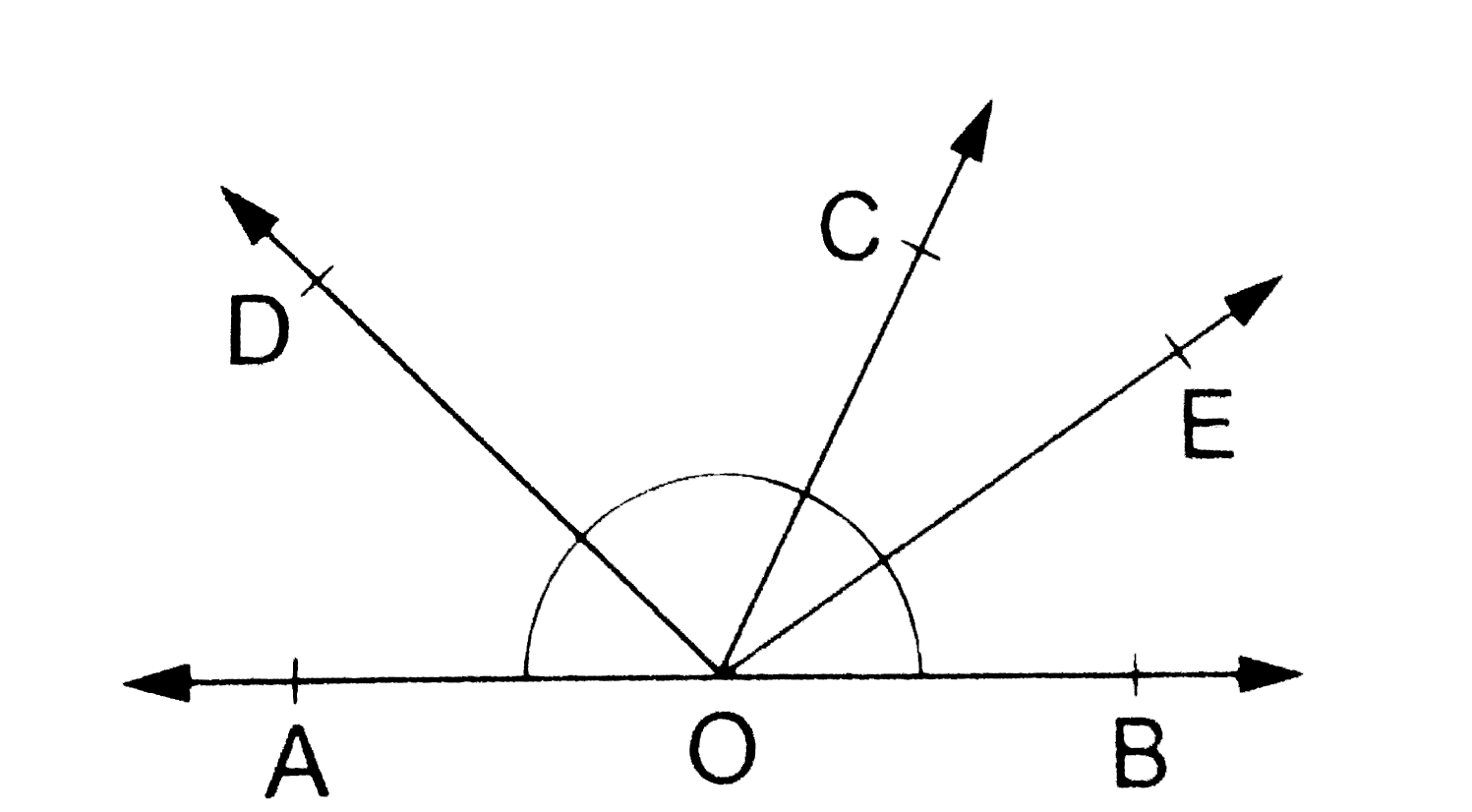 View Solution
View SolutionIn the given figure, AOB is a straight line. ∠AOC=67∘ and OD is the bisector of ∠BOC. What is the value of ∠BOD in degrees.
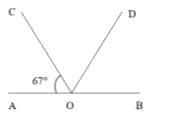 View Solution
View Solution

