In the given figure side of square ABCD is 7 cm.
With centre D and radius DA, sector D-AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region.
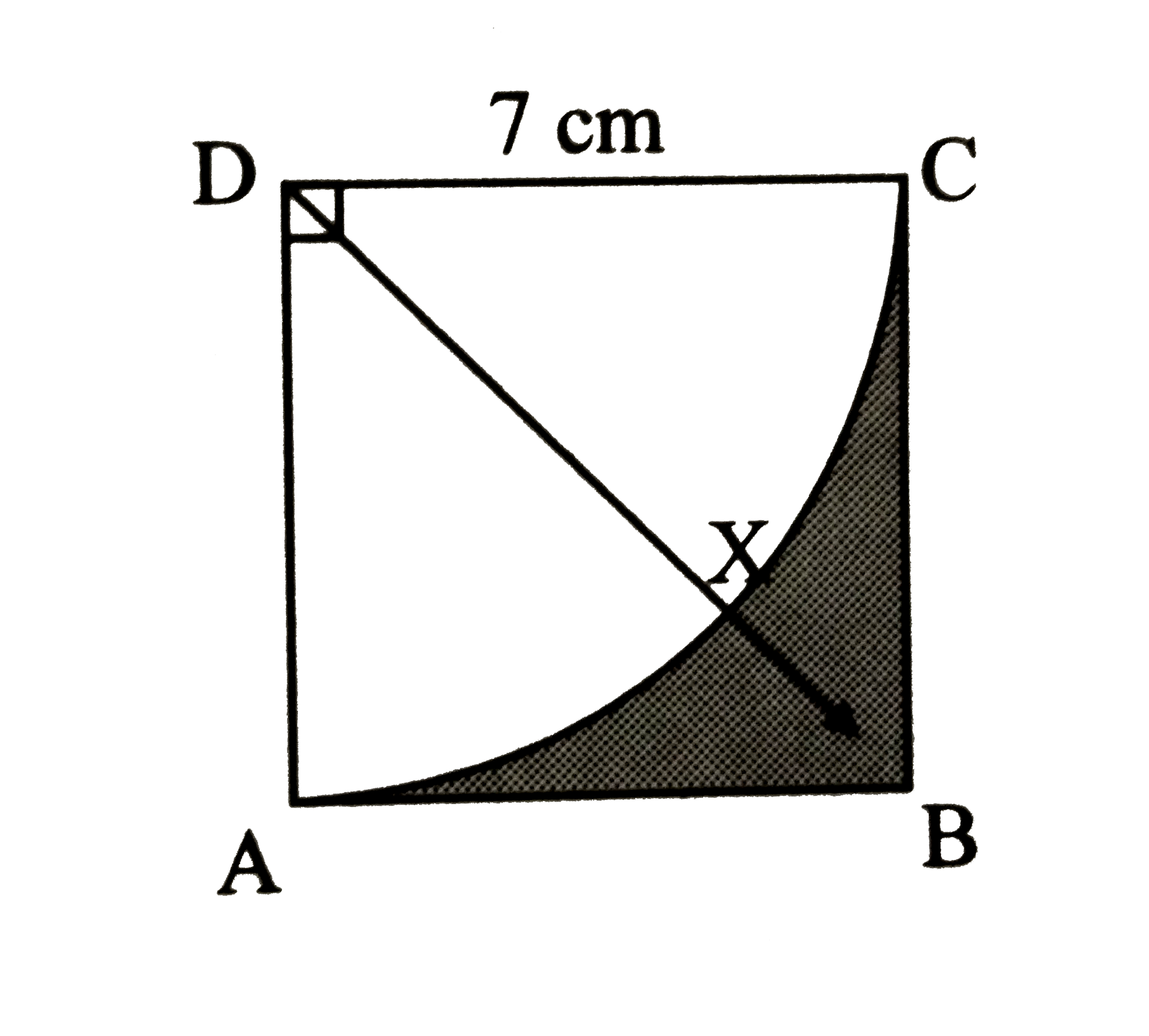
The correct Answer is:Area of a square =s^(2)
=72
=49cm2
Area of sector (D-AXC) =θ360×πr2 ...[Formula]
=90360×227×7×7
=38.5cm2
∴ A (shaded redion) = Area of a square - Area of sector
=49cm2−38.5cm2
=10.5cm2
Step by step video & image solution for In the given figure side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Textual Activity1videos
MENSURATION
- BOOK - TARGET PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Additional Problems for Practice (Based on Practice Set 7.4)6videos
MENSURATION
- BOOK - TARGET PUBLICATIONCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Chapter Assessment20videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPEREXERCISE - Questions23videos
MODEL QUESTION PAPER
Similar Questions
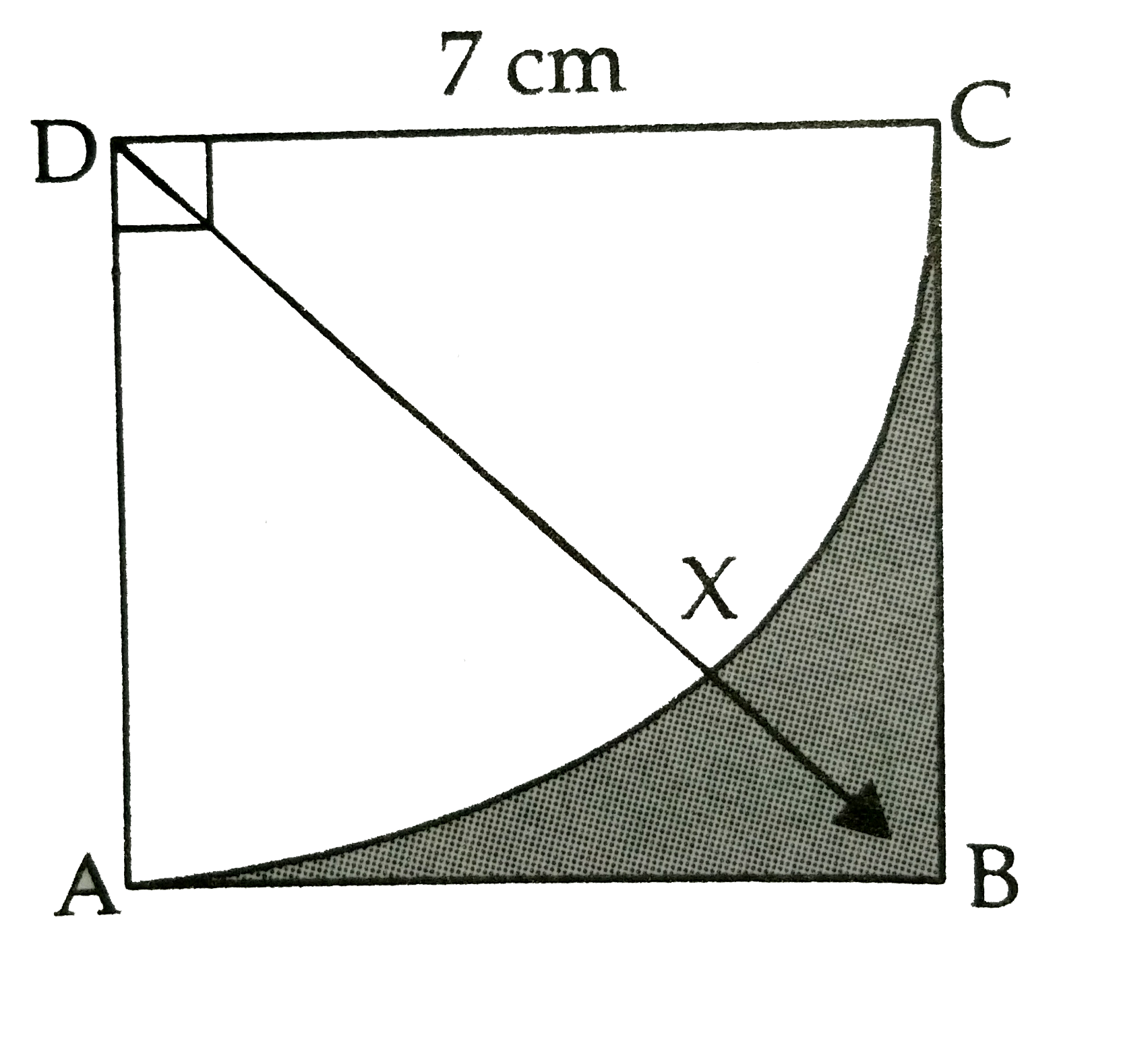
In the given figure, side of square ABCD is 7cm. With centre D and radius DA, sector D-AXC is drawn. Fill in the following boxes properly and find out the area of the shaded region.
 View Solution
View SolutionIn the given figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. find out the area of the shaded ragion.
View Solution
Knowledge Check
- Question 1 - Select One
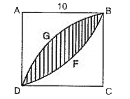
In the given figure, ABCD is a square with side 10 cm. BFD is an arc of a circle with centre C and BGD is an arc of a circle with centre A. What is the area of the shaded region in square centimetres ?
 A100−50πB100–25πC50π−100D25π–100
A100−50πB100–25πC50π−100D25π–100
In the figure, side of square ABCD is 7 cm. With centre D and radius DA, sector D-AXC is drawn. Find the area of the shaded region.
 View Solution
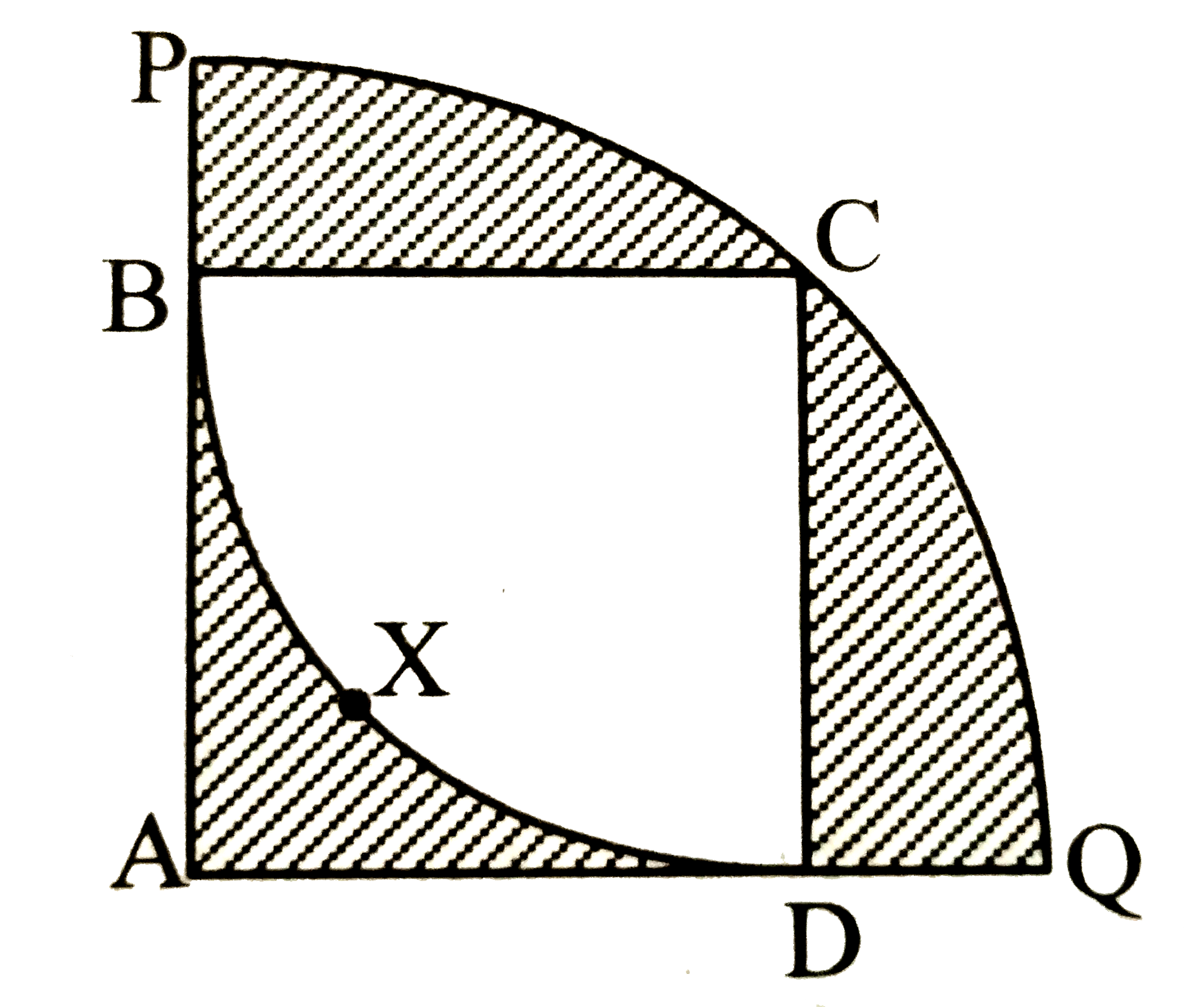
View SolutionIn the figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of the shaded portion.
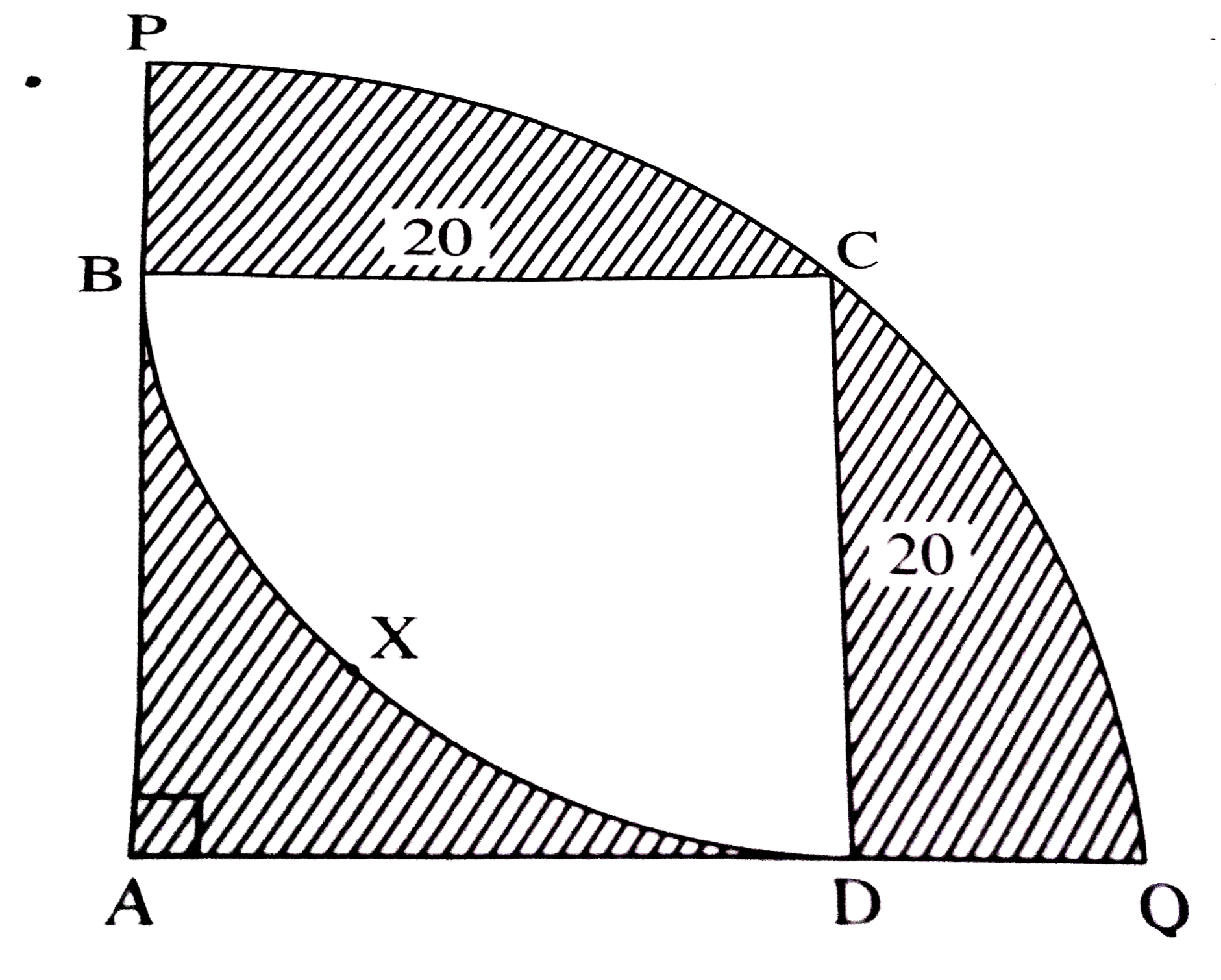
Side of the square ABCD = radius of sector C-BXD = 20 cm
Area of square =side2=400cm2
Area of sector C-BXD =θ360×πr2
=□360×3.14×202=□cm2
Area of the shaded portion inside square
= Area of square - A (sector C- BXD)
=400−□cm2
Radius of sector A-PCQ= Length of diagonal of square ABCD
r1=20√2cm
Area of the shaded region outside square
= A(sector A-PCQ)-A (square ABCD)
=90360×3.14×(20√2)2−200
=□cm2
∴ total area of shaded portion = area of shaded portion inside square + area of shaded portion outside square =□cm2View SolutionSide of square ABCD is 7 cm with D as the centre and DA as radius, arc XC is drawn. Find the area of the shaded region with the help of the following flow chart.

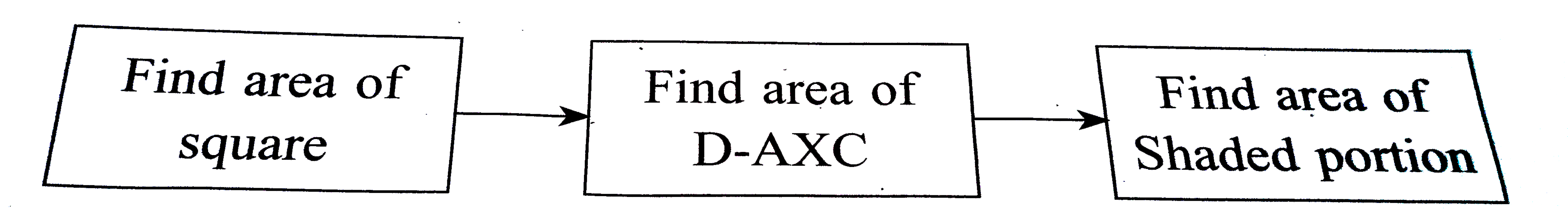 View Solution
View SolutionIn the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.
 View Solution
View SolutionIn the figure, square ABCD is inscribed in the sector A-PCQ. The radiuys of sector C-BXD is 20 cm. Find the area of shaded region.
 View Solution
View SolutionIn the given figure, the side of square is 28 cm and radius of each circle is half of the length of the sides of the square where O and O' are centres of the circles. Find the area of shaded region
View SolutionIn Figure ABCD is a square with side 7 cm. A circle is drawn circumscribing the square . Find the area of the shaded region .
 View Solution
View Solution

