In the given figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side AB=42m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find
(i) the sum of the areas of the lawn and flower beds,
(ii) the sum of the areas of two flower beds.
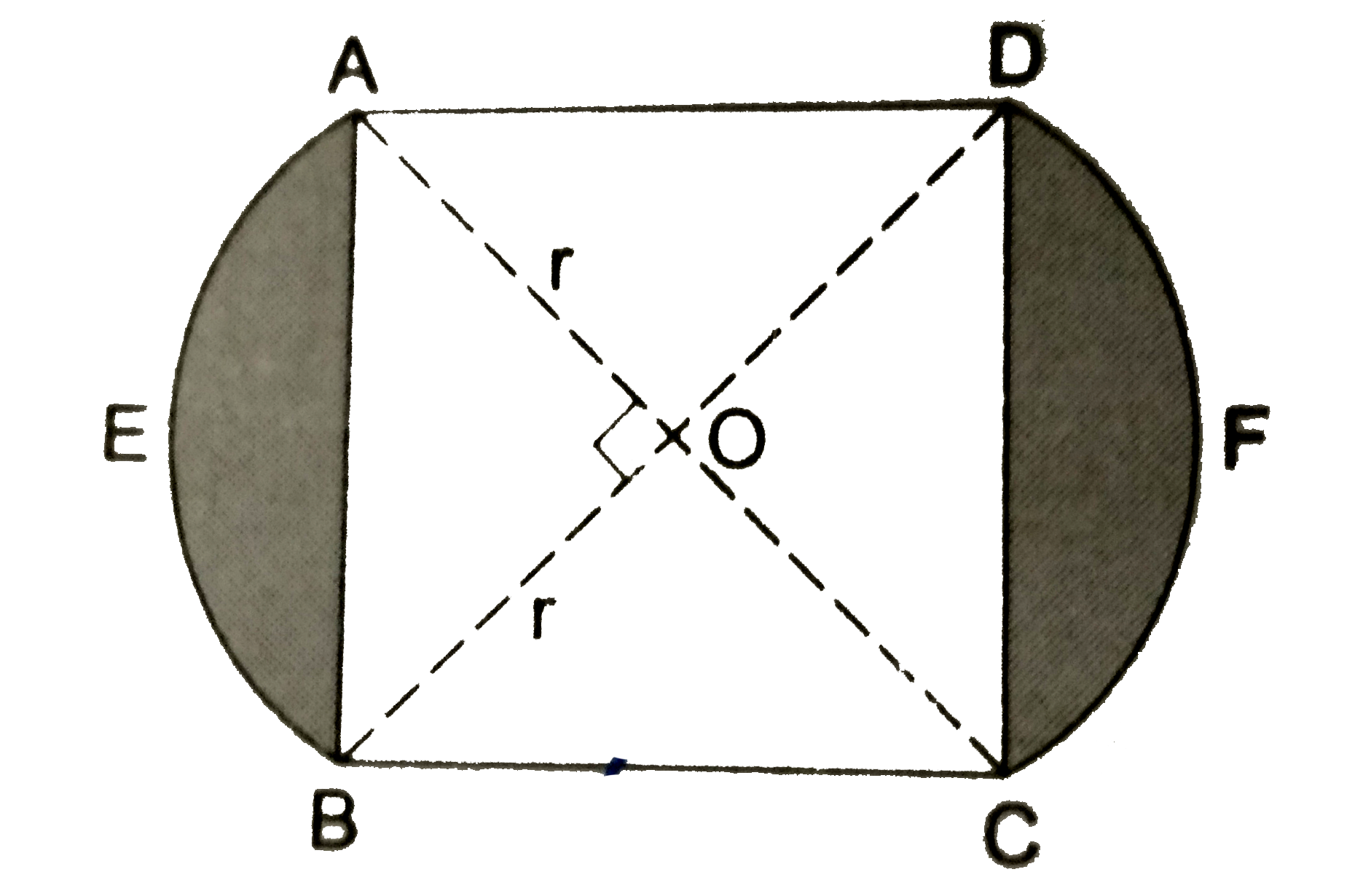
Area of the square lawn ABCD =(42×42)m2
Let OA=OB=r metres. Then ∠AOB=90∘
∴OA2+OB2=AB2⇒r2+r2=(42)2
⇒2r2=1764⇒r2=882
(i) Sum of the areas of the lawn and the flower beds
= ar(sector OAEBO) + ar(sector OCFDO)
+ar(ΔOAD)+ar(ΔOBC)
=(227×882×90360)m2+(227×882×90360)m2
+(12×r×r)m2+(12×r×r)m2
=2{(227×882×90360)+12r2}m2
=2{693+12×882)m2=2(693+441)m2
=2268m2
Hence the sum of the areas of the lawn and the two flower bed sis 2268m2
(ii) Sum of the areas of the two flower beds
=2{ar(sectorOAEBO)−ar(ΔOAB)}
=2(693−12×882)m2=2(693−441)m2
=504m2
Topper's Solved these Questions
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - SOLVED EXAMPLE_TYPE
1 Videos
- AREA OF CIRCLE, SECTOR AND SEGMENT BOOK - RS AGGARWALCHAPTER - AREA OF CIRCLE, SECTOR AND SEGMENT EXERCISE - Exercise 16A
65 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
Similar Questions
In Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionIt is proposed to add to a square lawn measuring 58cm on a side, two circalar ends. The centre of each circle is the point of intersection of the diagonals of the square. Find the area of the whole lawn.
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionEach side of a square flower bed is 2 m 80 cm long. It is extended by digging a strip 30 cm wide all around it. Find the area of the enlarged flower bed and also the increase in the area of the flower bed.
View SolutionThe sum of the areas of two squares is 157m2 . If the sum of their perimeters is 68 m , find the sides of the two squares .
View SolutionThe side of a square exceeds the side of the another square by 4 cm and the sum of the areas of the two squares is 400 sq. cm. Find the dimensions of the squares.
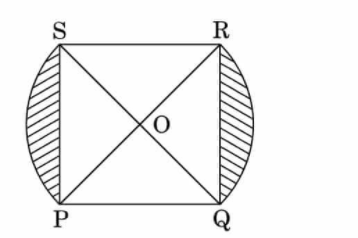
View Solution. In the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its diagonals. Find the total area of the two flower beds (shaded parts).
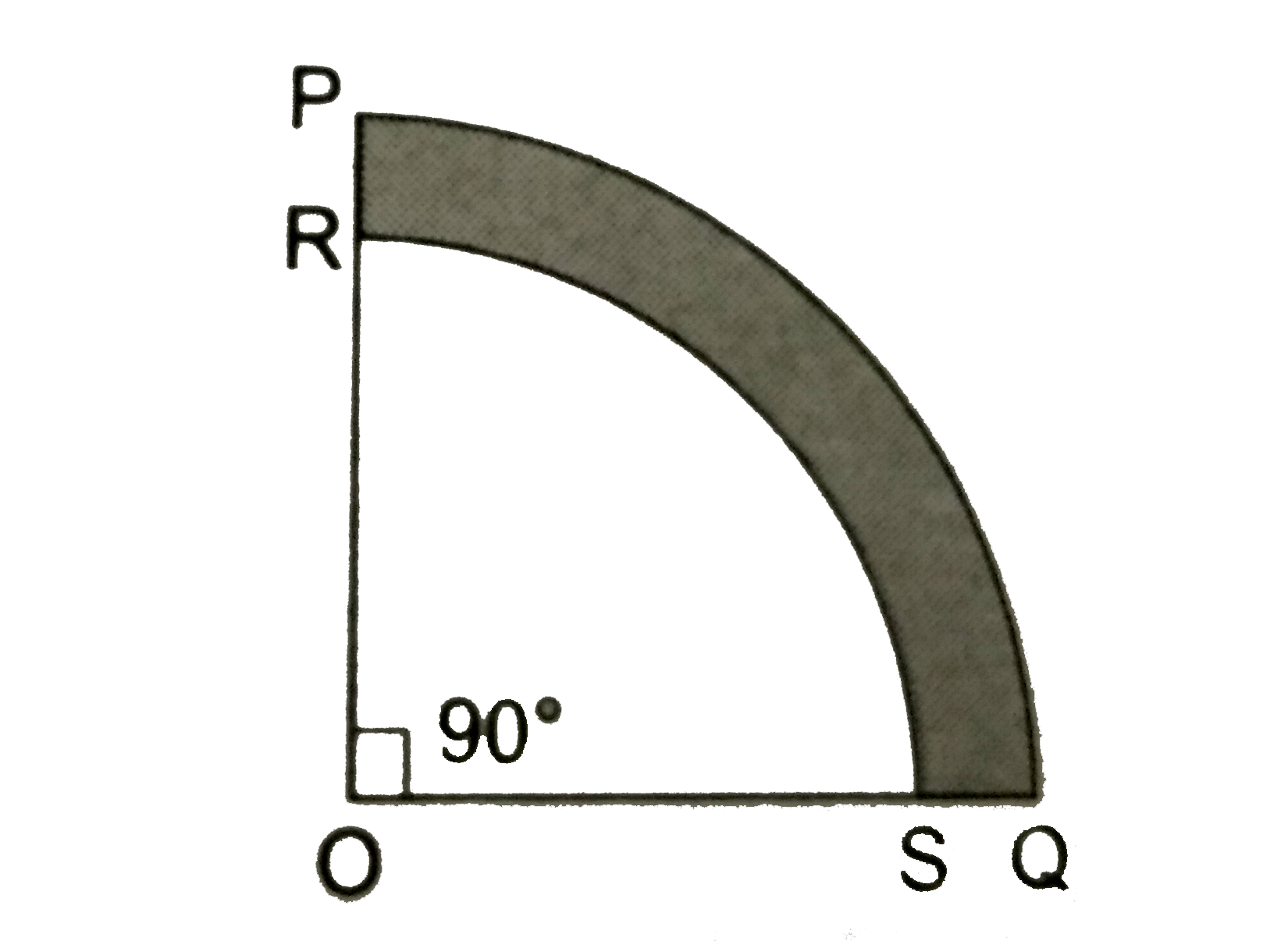
View SolutionIn the given figure, PQSR represents a flower bed. If OP=21m and OR=14m, find the area of the flower bed.
View SolutionTwo squares have sides xcm and (x+4) . The sum of their areas is 656cm2 . Find the sides of the squares.
View Solution
