In the standard (x,y) coordinate plane, the circle centerd at (1,3) that passes through (4,7) is the set of all points that are:
5 coordinate units from (1,3)
5 coordinate units from both (1,3) and (4,7)
5 coordinate units from the line segment with endpoints (1,3) and (4,7)
equidistant from (1,3) and (4,7)
The correct Answer is:A
To solve the problem, we need to find the equation of the circle centered at (1, 3) that passes through the point (4, 7). Here are the steps to derive the solution:
Step 1: Identify the center of the circle
The center of the circle is given as (1, 3).
Step 2: Find the radius of the circle
To find the radius, we need to calculate the distance between the center (1, 3) and the point (4, 7) using the distance formula:
r=√(x2−x1)2+(y2−y1)2
Here, (x1,y1)=(1,3) and (x2,y2)=(4,7).
Substituting the values:
r=√(4−1)2+(7−3)2
=√(3)2+(4)2
=√9+16
=√25
=5
So, the radius r is 5 units.
Step 3: Write the equation of the circle
The standard equation of a circle with center (h,k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting h=1, k=3, and r=5:
(x−1)2+(y−3)2=52
(x−1)2+(y−3)2=25
Step 4: Interpret the result
The equation (x−1)2+(y−3)2=25 represents all points (x,y) that are 5 units away from the center (1, 3). Therefore, the set of all points that satisfy this equation forms a circle with a radius of 5 centered at (1, 3).
Final Answer
The circle centered at (1, 3) that passes through (4, 7) is the set of all points that are 5 coordinate units from (1, 3).
---
The center of the circle is given as (1, 3).
To find the radius, we need to calculate the distance between the center (1, 3) and the point (4, 7) using the distance formula:
r=√(x2−x1)2+(y2−y1)2
Here, (x1,y1)=(1,3) and (x2,y2)=(4,7).
r=√(4−1)2+(7−3)2
=√(3)2+(4)2
=√9+16
=√25
=5
So, the radius r is 5 units.
The standard equation of a circle with center (h,k) and radius r is given by:
(x−h)2+(y−k)2=r2
Substituting h=1, k=3, and r=5:
(x−1)2+(y−3)2=52
(x−1)2+(y−3)2=25
The equation (x−1)2+(y−3)2=25 represents all points (x,y) that are 5 units away from the center (1, 3). Therefore, the set of all points that satisfy this equation forms a circle with a radius of 5 centered at (1, 3).
The circle centered at (1, 3) that passes through (4, 7) is the set of all points that are 5 coordinate units from (1, 3).
Topper's Solved these Questions
Similar Questions
Knowledge Check
When points A and B (-3, 4) are graphed in the standard (x,y) coordinate plane below, the midpoint of ¯¯¯¯¯¯AB will be (1,2). What will be the coordinate of point A?
 A(−7,6)B(−2,1)C(−1,3)D(5,0)
A(−7,6)B(−2,1)C(−1,3)D(5,0)In the standard (x, y) coordinate plane, what is the slope of the line segement joining the points (3, -5) and (7, 2) ?
A−74B−34C34D74Consider the functions f(x)=√x and g(x)x2−b. In the standard (x, y) coordinate plane, y=f(g(x)) passes through the point (3, 5). What is the value of b ?
A16B4C−2D−16
The function g(x)=x4−2x3−6x2−x+5 and line h are shows in the standard (x,y) coordinate plane below . Which of the following is an equation of line h , which passes through (-1,3) and (2,-21) ?
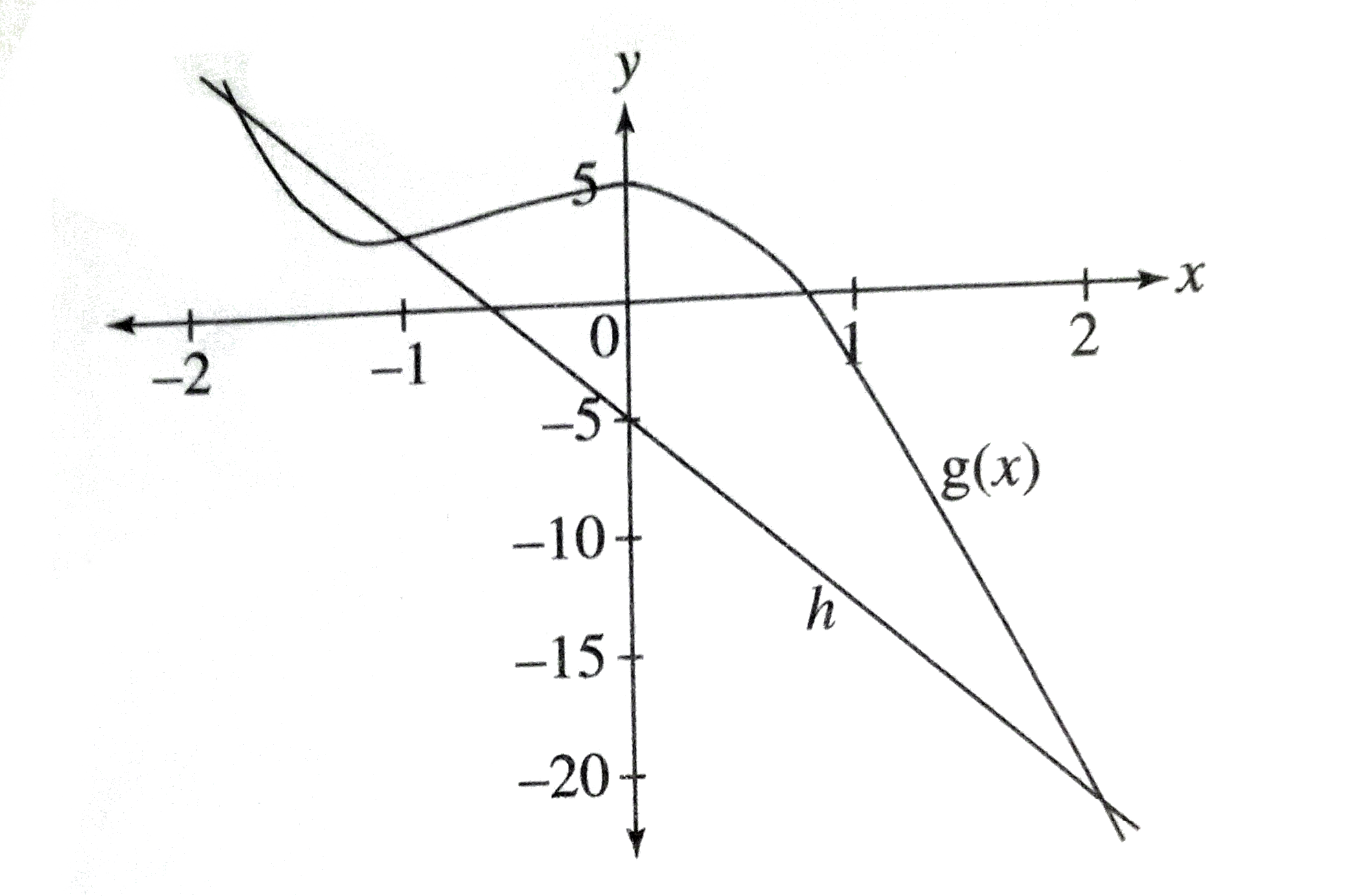
View SolutionWhich of the following values is the x-coordinate of the point in the standard (x,y) coordinate plane where the graph of the line y = 7 intersects the graph of the function y=1n(x−2)+3?
View SolutionThe function y=f(x) is graphed in the standard (x, y) coordinate plane below.

The points on the graph of the function y=3+f(x−1) can be obtained from the points on y=f(x) by a shift of:
View SolutionAs shown below, the diagonals of rectange EFGH intersect at the point (-2,-4) in the standard (x,y) coordinate plane. Point F is at (-7,-2) . Which of the following are the coordinates of H ?
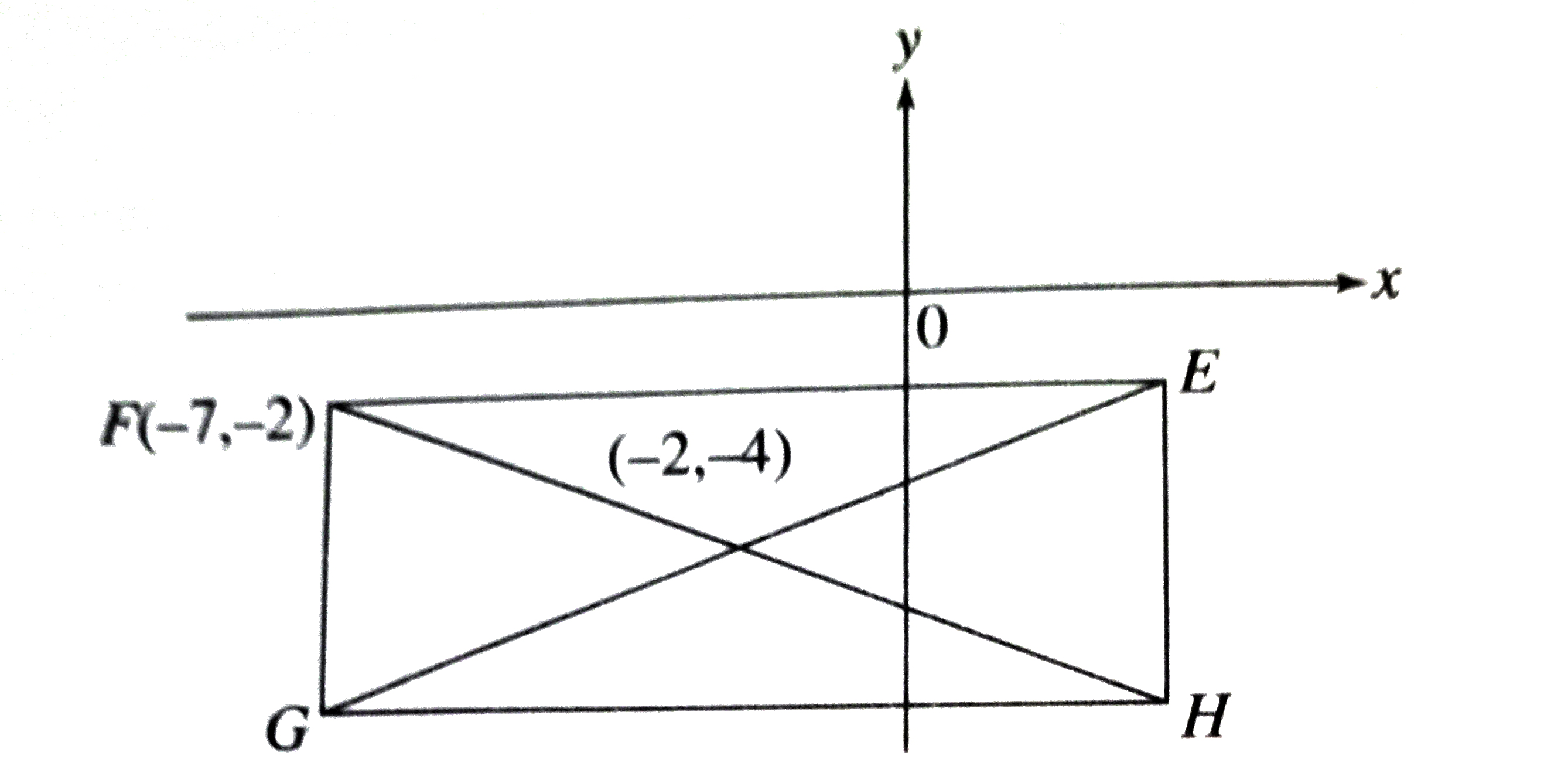
View SolutionWhat is the y-intercept of the line in the standard (x,y) coordinate plane that goes through the points (-3,6) and (3,2) ?
View Solution
