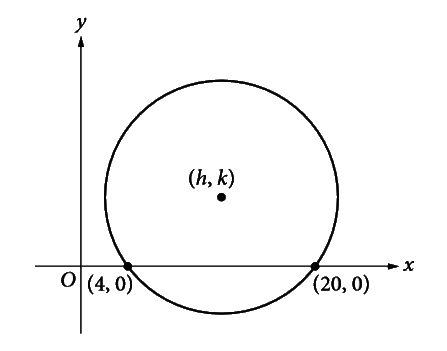
In the xy-plane above, the circle has center (h, k) and radius 10. What is the value of k ?
The correct Answer is:6
Circles are symmetric with respect to any given diameter through the center (h, k). One diameter of the circle is perpendicular to the x-axis. Therefore, the value of h is the mean of the x-coordinates of the circle’s two x-intercepts: h = 20+42=12. The radius of the circle is given as 10, so the point (h, k) must be a distance of 10 units from any point on the circle. The equation of any circle can be written as (x−h)2+(y−k)2=r2, where (h, k) is the center of the circle and r is the length of the radius of the circle. Substituting 12 for h and 10 for r into this equation gives (x−12)2+(y−k)2=102. Substituting the x-coordinate and y-coordinate of a point on the circle, (4, 0), gives (4−12)2+(0−k)2=102, or 64+k2=100. Subtracting 64 from both sides of this equation yields k2 = 36. Therefore, k=±√36 . Since the graph shows the point (h, k) in the first quadrant, k must be the positive square root of 36, so k = 6.
Similar Questions
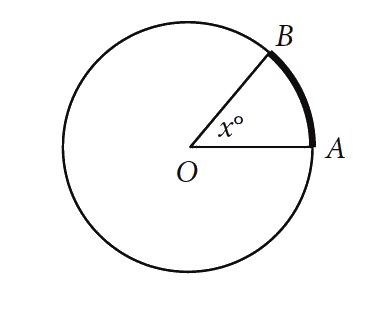
Note: Figure not drawn to scale.
In the figure above, the circle has center O and has radius 10. If the length of arc (shown in bold) is between 5 and 6, what is one possible integer–––––––– value of x ?
(shown in bold) is between 5 and 6, what is one possible integer–––––––– value of x ?
View Solution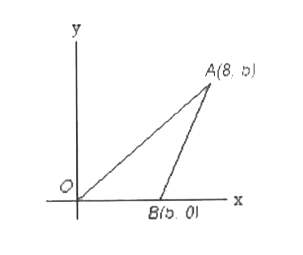
In the xy - plane above, the area of triangle OAB is 32. What is the value of b?
View Solution
Knowledge Check

In the figure above, the circle has center A, and BC=AB. What is the degree measure of the marked angle?A60∘B270∘C300∘D340∘
In the xy-plane above, the circle has center O, and the measure of ∠XOY is πn radians. What is the value of n?A1B3C6D12In the xy-plane , a circle with center (6,0) is tangent to the line y=x. what is the radius of the circle ?
A2√6B2√3C3√2D3
The graph of g(x)=(3x−9)(x−1) is a parabola in the xy-plane. If the vertex of this parabola has coordinates (h, k), what is the value of h−k?
View Solutionx2+y2+4x−10y−20=0
The graph of the equation above is a circle with center (h, k) and radius r. Computer. r.(k−h).
View Solution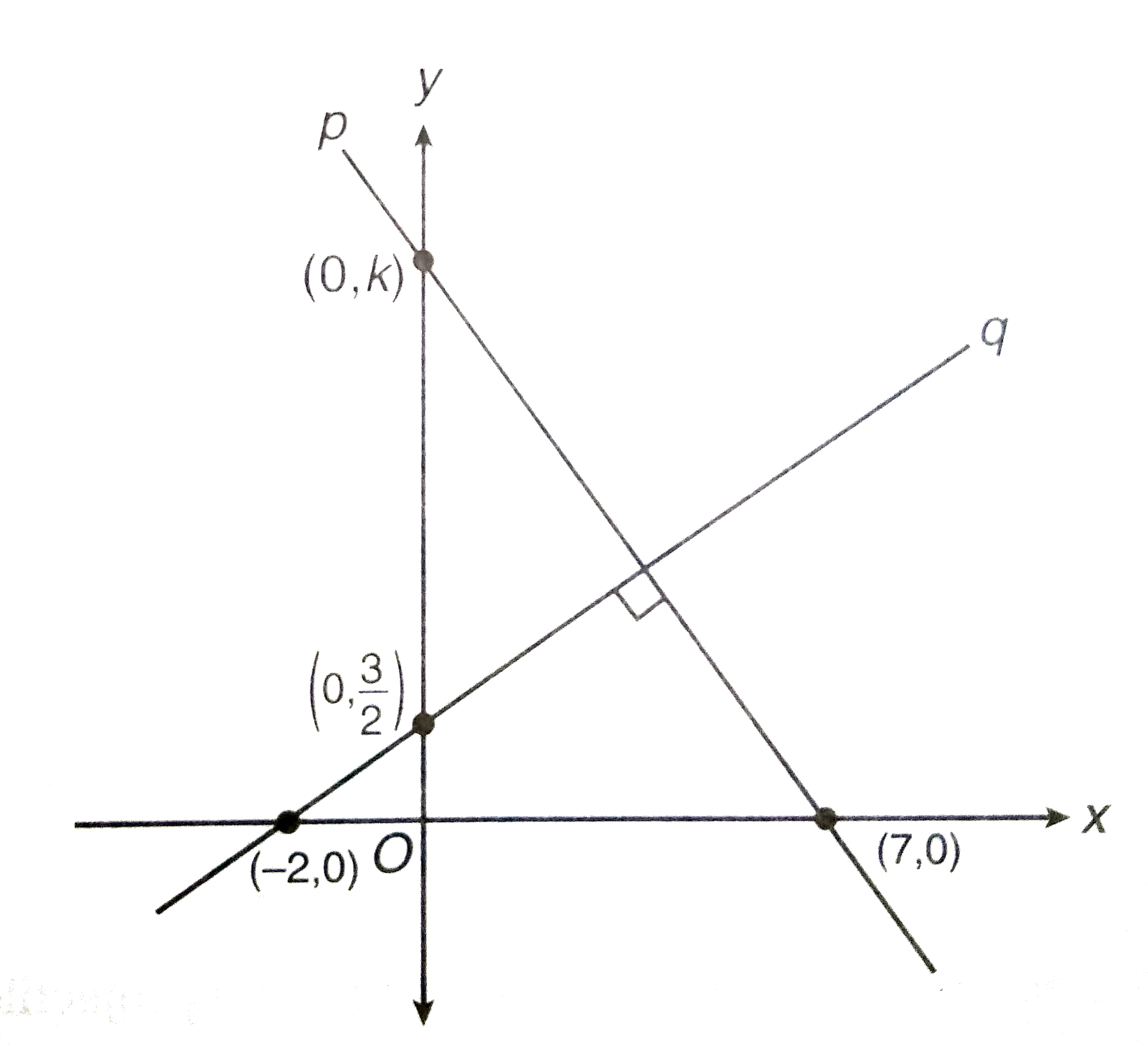
In the xy-plane above, line p is perpendicular to line q. What is the value of k?
View Solution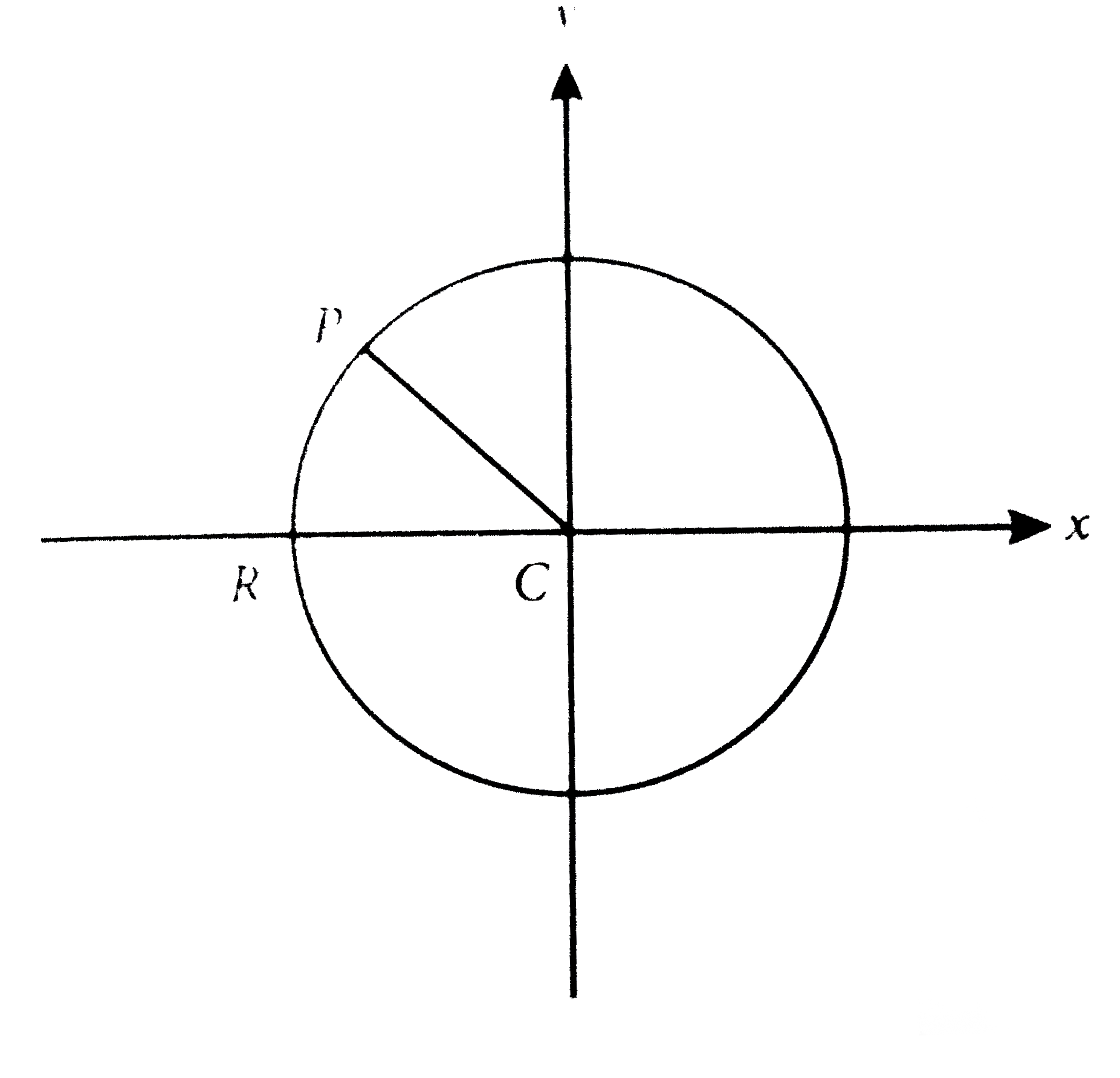
In the xy-plane above, the circle with center C contains the point P with coordinates (−√2,√2). If angle PCR has a measure of πx radians, what ist he value of x?
View SolutionA circle in the xy -plane has center ( 5, 7) and radius 2. Which of the following is an equation of the circle?
View Solution
