In triangle ABC, angle C measures 90∘. If cosB=1213, what is the value of sinB?
512
513
1213
1312
The correct Answer is:B
To find the value of sinB in triangle ABC where angle C is 90∘ and cosB=1213, we can use the Pythagorean identity:
1. Use the Pythagorean Identity:
The Pythagorean identity states that:
cos2B+sin2B=1
2. Substitute the value of cosB:
Given cosB=1213, we can find cos2B:
cos2B=(1213)2=144169
3. Plug cos2B into the identity:
Substitute cos2B into the Pythagorean identity:
144169+sin2B=1
4. Isolate sin2B:
To find sin2B, rearrange the equation:
sin2B=1−144169
5. Convert 1 to a fraction with the same denominator:
Convert 1 to a fraction:
1=169169
Now substitute:
sin2B=169169−144169=25169
6. Take the square root:
To find sinB, take the square root of both sides:
sinB=√25169=513
7. Consider the positive value:
Since B is an angle in a triangle, we take the positive value:
sinB=513
Final Answer:
sinB=513
The Pythagorean identity states that:
cos2B+sin2B=1
Given cosB=1213, we can find cos2B:
cos2B=(1213)2=144169
Substitute cos2B into the Pythagorean identity:
144169+sin2B=1
To find sin2B, rearrange the equation:
sin2B=1−144169
Convert 1 to a fraction:
1=169169
Now substitute:
sin2B=169169−144169=25169
To find sinB, take the square root of both sides:
sinB=√25169=513
Since B is an angle in a triangle, we take the positive value:
sinB=513
sinB=513
Topper's Solved these Questions
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #6
3 Videos
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #7
3 Videos
- ADDITIONAL TOPICSBOOK - PRINCETONCHAPTER - ADDITIONAL TOPICSEXERCISE - QUICK QUIZ #4
3 Videos
- ADVANCED ARITHMETICBOOK - PRINCETONCHAPTER - ADVANCED ARITHMETICEXERCISE - Examples
25 Videos
Similar Questions
Knowledge Check
In a right triangle, on angle measure y∘, where cosy=35. What is the sin(90∘−y∘)?
A35B34C45D43A triangle whose angles measure 35∘,55∘and90∘ is
Aacute angledBright angledCobtuse angledDnone of theseIn the diagram below ,ΔABC is isosceles and ΔBCD is equilateral . ¯¯¯¯¯¯AB=¯¯¯¯¯¯BC and the measure of ∠ABC is half the measure of ∠BAC. what is the measure of ∠ABD ?
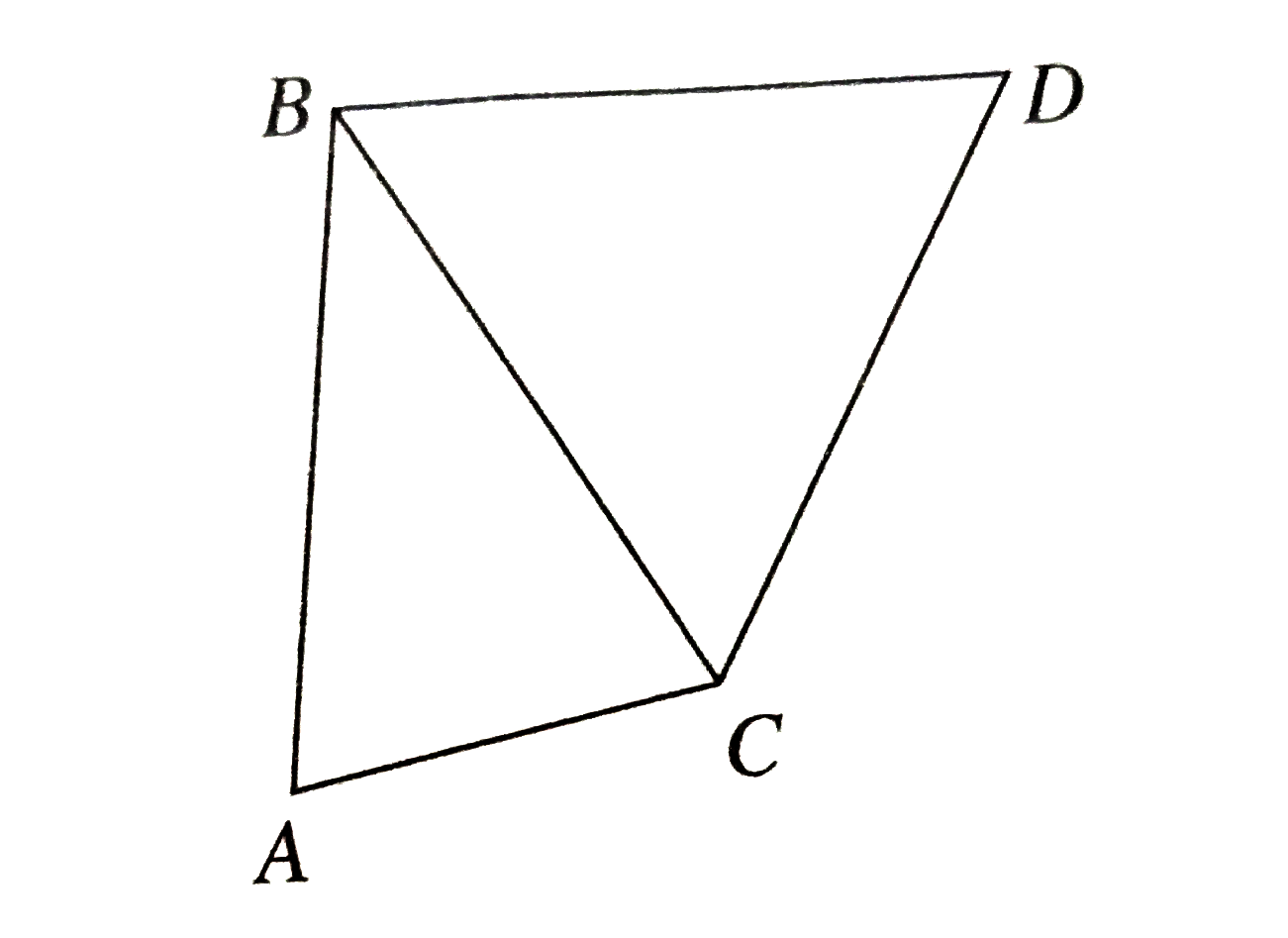 A36∘B60∘C72∘D96∘
A36∘B60∘C72∘D96∘
In a triangle ABC, ∠A=60∘andb:c=(√3+1):2, then find the value of (∠B−∠C)
View SolutionIn triangle ABC, the measure of ∠B is 90∘, BC = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 13 the length of the corresponding side of triangle ABC. What is the value of sin F ?
View SolutionIf the lengths of the sides of a right- angled triangle ABC, right angled at C, are in arithmetic progression, then the value of 5(sinA+sinB) is
View SolutionIn a right triangle, one angle measure x∘, where sinx∘=515. What is cos(90∘−x∘)?
View SolutionIn a right triangle, one angle measures x∘, where sinx∘=45. What is cos(90∘−x∘)?
View Solution
