In triangle ABC, let AD, BE and CF be the internal angle bisectors with D, E and F on the sides BC, CA and AB respectively. Suppose AD, BE and CF concur at I and B, D, I, F are concyclic, then ∠IFD has measure-
A
15∘
B
30∘
C
45∘
D
Any value ≤90∘
Video Solution
Text Solution
The correct Answer is:B
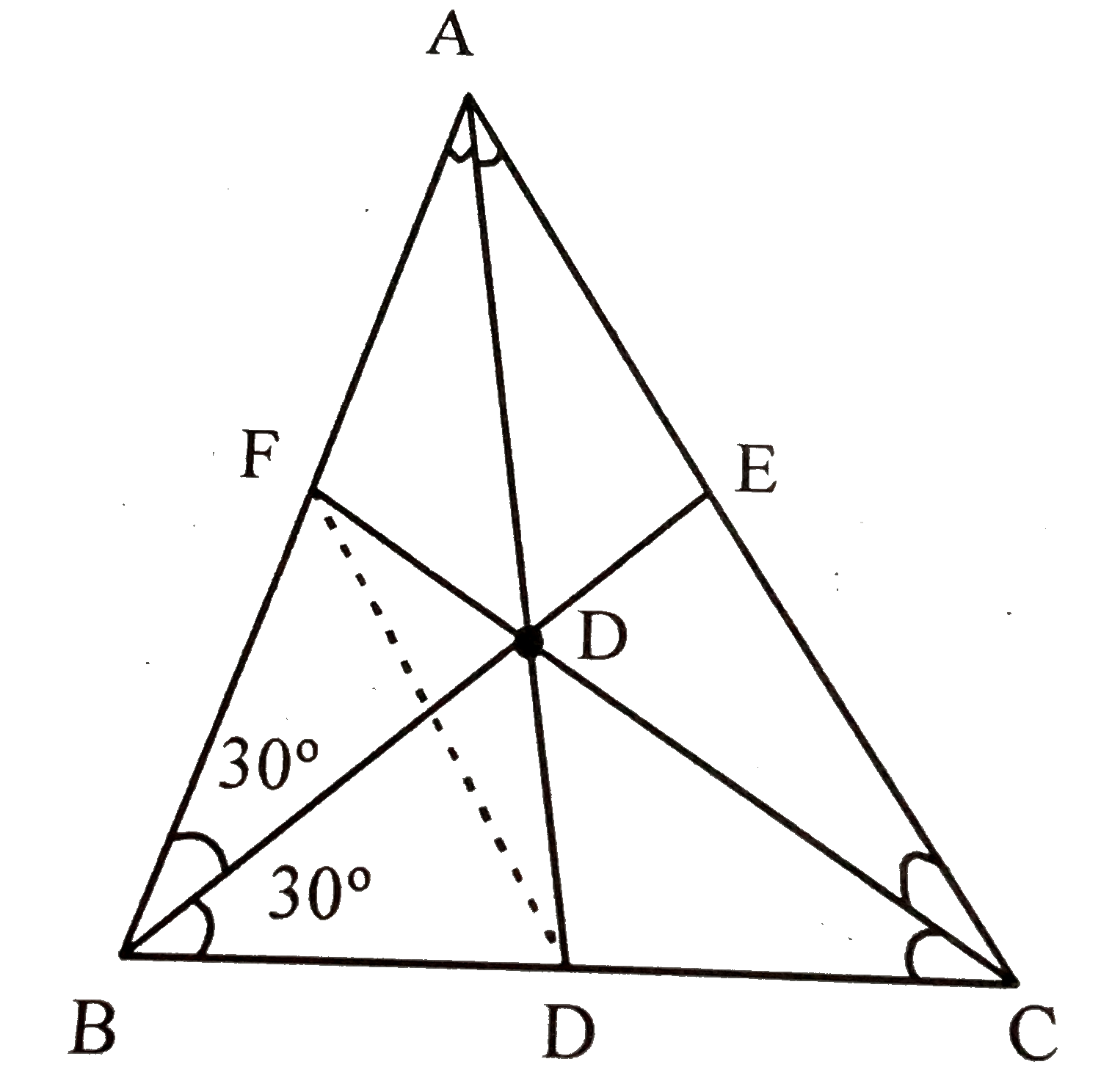
∠AIC=180∘−(A+C2)
180∘−(A+C2)
=90∘+B2
Here:- =90∘+B2+B=180∘
B=60∘
This will be case of equilateral Δ
|
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHEMATICS
5 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - exercise
18 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CFIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF
If D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionLet ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
"
View SolutionThe in circle of ΔABC touches the sides BC, CA and AB at D, E and F respectively. Then AF + BD + CE is equal to :
View SolutionIn △ABC, AD is the internal bisector of ∠S, meeting the side BC at D. If BD = 5cm, BC = 7.5 cm, then AB:AC is:
View SolutionLet D, E, F be the middle points of the sides BC, CA, AB respectively of a triangle ABC. Then →AD+→BE+→CF equals
View Solution
