In △ABC (not shown), AC⊥BCadcos∠ABC=1213. What is the value of tan∠ABC?
513
512
1213
125
The correct Answer is:B
To find the value of tan∠ABC in triangle ABC where AC is perpendicular to BC and cos∠ABC=1213, we can follow these steps:
Step 1: Understand the relationship of cosine in a right triangle
In a right triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the hypotenuse. Here, cos∠ABC=BCAB.
Step 2: Assign values based on cosine
From the given cos∠ABC=1213, we can assign:
- BC=12 (adjacent side)
- AB=13 (hypotenuse)
Step 3: Use the Pythagorean theorem to find the opposite side
We need to find the length of the opposite side AC. According to the Pythagorean theorem:
AB2=BC2+AC2
Substituting the known values:
132=122+AC2
Calculating the squares:
169=144+AC2
Now, isolate AC2:
AC2=169−144
AC2=25
Taking the square root gives:
AC=5
Step 4: Calculate tan∠ABC
Now that we have AC (the opposite side) and BC (the adjacent side), we can find tan∠ABC:
tan∠ABC=ACBC=512
Final Answer
Thus, the value of tan∠ABC is 512.
---
In a right triangle, the cosine of an angle is defined as the ratio of the length of the adjacent side to the hypotenuse. Here, cos∠ABC=BCAB.
From the given cos∠ABC=1213, we can assign:
- BC=12 (adjacent side)
- AB=13 (hypotenuse)
We need to find the length of the opposite side AC. According to the Pythagorean theorem:
AB2=BC2+AC2
Substituting the known values:
132=122+AC2
Calculating the squares:
169=144+AC2
Now, isolate AC2:
AC2=169−144
AC2=25
Taking the square root gives:
AC=5
Now that we have AC (the opposite side) and BC (the adjacent side), we can find tan∠ABC:
tan∠ABC=ACBC=512
Thus, the value of tan∠ABC is 512.
Topper's Solved these Questions
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:Geometry Drill 2: Calculator-Permitted Section
Explore 8 Videos
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:EXAMPLES
Explore 13 Videos
- FUNCTIONS AND GRAPHSBook:PRINCETONChapter:FUNCTIONS AND GRAPHSExercise:Functions and Graphs Drill 2: Calculator -Permitted Section
Explore 6 Videos
- GRID-INSBook:PRINCETONChapter:GRID-INSExercise:Grid-In Drill 2: Calculator-Permitted Section
Explore 6 Videos
Similar Questions
Knowledge Check
In △ABC (not shown), ∠ABC=60∘andAC⊥BC. If AB=x, then what is the area of △ABC, in terms of x?
Ax2√38Bx2√34Cx2√32Dx2√3In the figure, AD and BC are lines intersecting at O.What is the value of a?
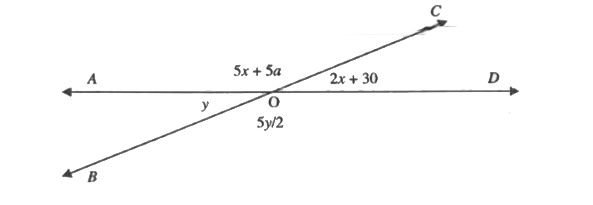 A15B30C45D60
A15B30C45D60
What is the value of 6tan2θ−6cos2θ ?
View Solution△ABC is right angled at A and AD⊥BC. If BC = 13 cm and AC= 5 cm. find the ratio of the areas of △ABCand△ADC.
View SolutionIf ab−3=12and2bc=5, what is the value of ac?
View Solution
In figure above, angles ACB and DEB are right angles, AC=15, DE=12, and DE=10. What is the value of cosx?
View Solution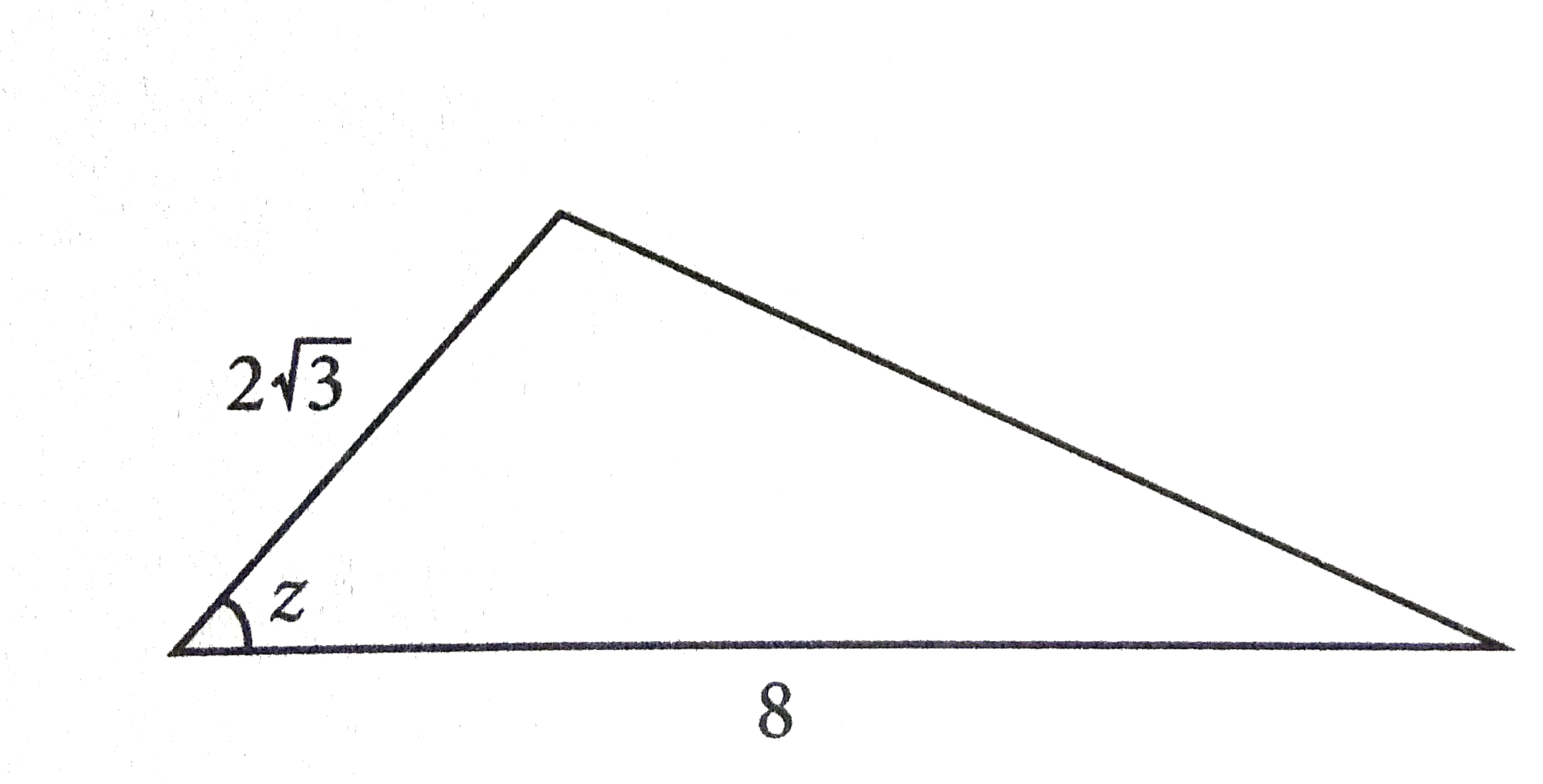
If the area of the triangle shown above is 12 squares inches, what is the value of cosz?
View SolutionIn ΔABC, if BC>AC>AB then :
(i) What is the relation ∠A and ∠C ?
(ii) What is the relation between the values of (AB+AC) and BC ?
(iii) What is the relation between the values of (AC−BC) and AB ?
(iv) What is the smallest angle in ΔABC ?
View Solution
