In △ABC,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the ΔOBC and quadrilateral AEOF are equal in area.
The correct Answer is:(i)80cm2andcm2 (ii) 240cm2and480cm2
Step by step video, text & image solution for In triangleABC,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the DeltaOBC and quadrilateral AEOF are equal in area. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
In ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
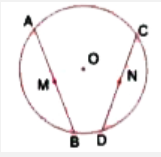
∠AMN=∠CNM.
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View Solution
