In △PQR, M and N are points on PQ and PR, respectively, such that ¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯QR, If PM =x, PR =x+9,PQ=x+13 and PN=x−2, then find x.
10
11
13
15
The correct Answer is:C
To solve the problem, we will use the properties of similar triangles, since ¯¯¯¯¯¯¯¯¯¯¯MN∥¯¯¯¯¯¯¯¯¯QR. This means that the triangles PMN and PQR are similar.
1. Identify the segments:
- Let PM=x
- PR=x+9
- PQ=x+13
- PN=x−2
2. Set up the ratio of the sides:
Since ¯¯¯¯¯¯¯¯¯¯¯MN∥¯¯¯¯¯¯¯¯¯QR, we can set up the following proportion based on the similarity of triangles:
PMPQ=PNPR
3. Substitute the values:
Substitute the values of PM, PQ, PN, and PR into the proportion:
xx+13=x−2x+9
4. Cross-multiply:
Cross-multiplying gives us:
x(x+9)=(x−2)(x+13)
5. Expand both sides:
Expanding both sides results in:
x2+9x=x2+13x−2x−26
Simplifying the right side:
x2+9x=x2+11x−26
6. Eliminate x2:
Subtract x2 from both sides:
9x=11x−26
7. Rearranging the equation:
Rearranging gives:
9x−11x=−26
−2x=−26
8. Solve for x:
Dividing both sides by -2:
x=13
Final Answer:
Thus, the value of x is 13.
- Let PM=x
- PR=x+9
- PQ=x+13
- PN=x−2
Since ¯¯¯¯¯¯¯¯¯¯¯MN∥¯¯¯¯¯¯¯¯¯QR, we can set up the following proportion based on the similarity of triangles:
PMPQ=PNPR
Substitute the values of PM, PQ, PN, and PR into the proportion:
xx+13=x−2x+9
Cross-multiplying gives us:
x(x+9)=(x−2)(x+13)
Expanding both sides results in:
x2+9x=x2+13x−2x−26
Simplifying the right side:
x2+9x=x2+11x−26
Subtract x2 from both sides:
9x=11x−26
Rearranging gives:
9x−11x=−26
−2x=−26
Dividing both sides by -2:
x=13
Thus, the value of x is 13.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
In △PQR L and M are two points on the sides PQ and PR respectively such that LMII QR. If PL = 2cm, LQ = 6 cm and PM= 1.5 cm, then MR (in cm) is
A0.5B4.5C9D8In a triangle PQR, S and T lie on PQ and PR, respectively, such that ∠QSR=∠PRQ and ∠QTR=∠PQR. And, PQ = 12, QR = 9, PR = 15. Find the value of PS×PT
AA)50.4BB)52.64CC)49.75DD)none of theseIn a ΔPQR, points M and N are on the sides PQ and PR respectively such that PM 0.6. PQ and NR=0.4PR. What percentage of the area of the triangle PQR does that of triangle PMN form?
A60%B50%C36%D55%
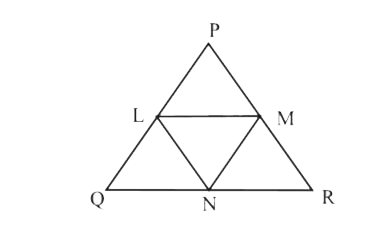
In the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View SolutionE and F are points on the sides PQ and PR respectively of a ΔPQR. Show that Ef||QR. If PQ = 1.28 cm,PR= 2.56 cm,PE = 0.18 cm and PF= 0.36 cm.
View Solution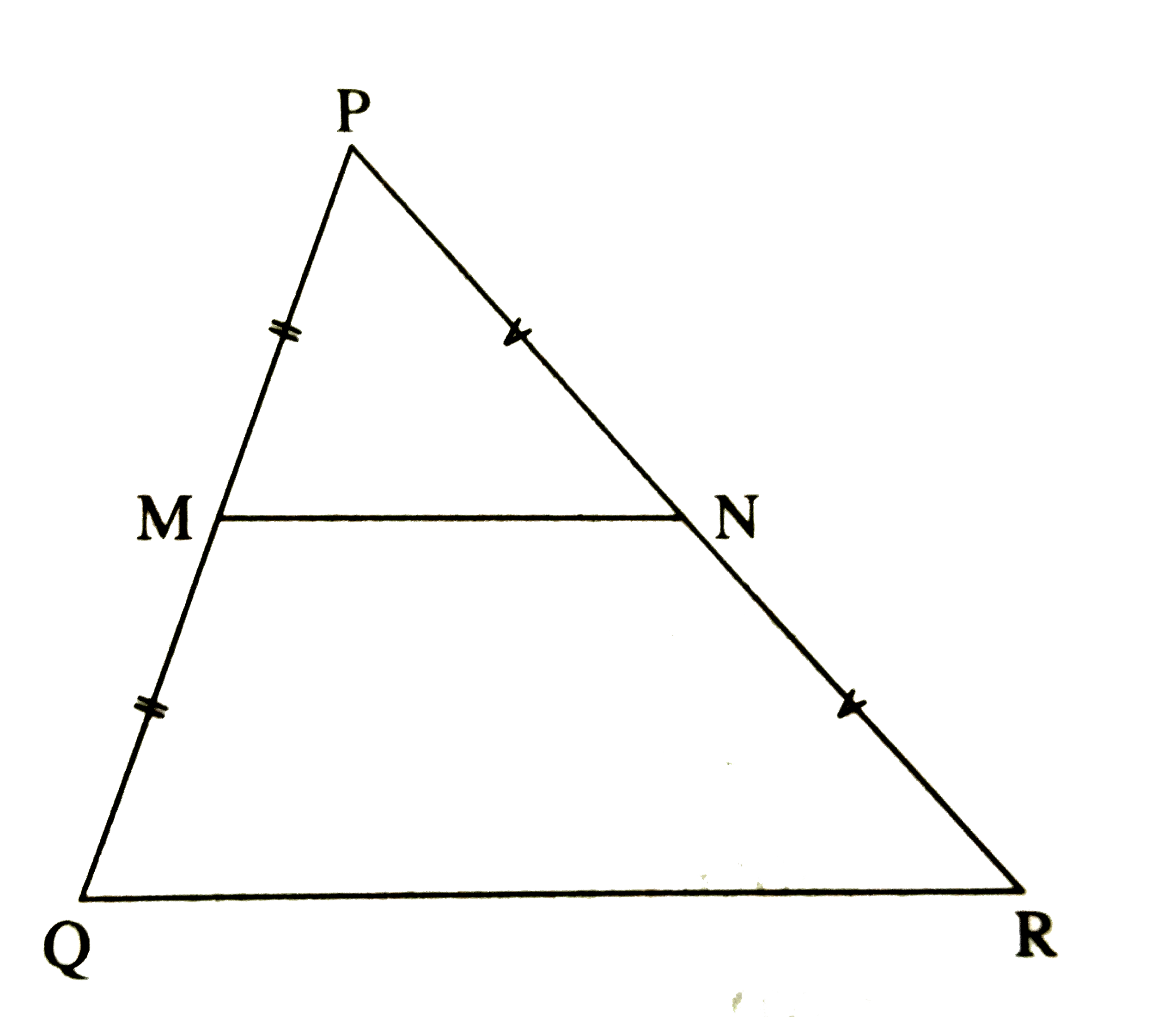
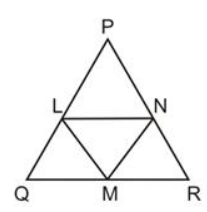
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .
View SolutionIn A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
View SolutionIn ΔPQR,right-angled at Q,X,Y and Z are points on sides PR,RQandPQrespectively such that QX⊥PR,XY⊥RQandXZ⊥PQ . Find the value of XZ If PZ=4cmandZQ=9cm.
View Solution