∫sinx+cosx√1+sin2xdx
The correct Answer is:N/a
To solve the integral
I=∫sinx+cosx√1+sin2xdx,
we can follow these steps:
Step 1: Rewrite the denominator
First, we note that sin2x=2sinxcosx. Thus, we can rewrite the expression under the square root:
1+sin2x=1+2sinxcosx.
Step 2: Use the Pythagorean identity
We can use the Pythagorean identity sin2x+cos2x=1 to rewrite 1:
1+2sinxcosx=sin2x+cos2x+2sinxcosx=(sinx+cosx)2.
Step 3: Substitute into the integral
Now substituting this back into the integral gives us:
I=∫sinx+cosx√(sinx+cosx)2dx.
Since √(sinx+cosx)2=|sinx+cosx|, we can assume sinx+cosx is positive in the interval we are considering (or we can handle the absolute value later).
Thus, we have:
I=∫sinx+cosxsinx+cosxdx=∫1dx.
Step 4: Integrate
Now, integrating 1 with respect to x:
I=x+C,
where C is the constant of integration.
Final Result
Thus, the final result of the integral is:
∫sinx+cosx√1+sin2xdx=x+C.
---
First, we note that sin2x=2sinxcosx. Thus, we can rewrite the expression under the square root:
We can use the Pythagorean identity sin2x+cos2x=1 to rewrite 1:
Now substituting this back into the integral gives us:
Now, integrating 1 with respect to x:
Thus, the final result of the integral is:
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTEGRALSEXERCISE - Long Answer13videos
INTEGRALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTEGRALSEXERCISE - Objective Type12videos
INTEGRALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - Objective1videos
DIFFERENTIAL EQUATIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers18videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
∫(sinx+cosx√sin2xdx
View SolutionEvaluate: ∫sinx−cosx√sin2xdx
View SolutionEvaluate the definite integrals∫π3π6sinx+cosx√sin2xdx
View Solution∫sinx−cosx√1−sin2xesinxcosxdx is equal to
View SolutionThe value of ∫sinx−cosx√sin2xdx is equal to
View SolutionOn a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).
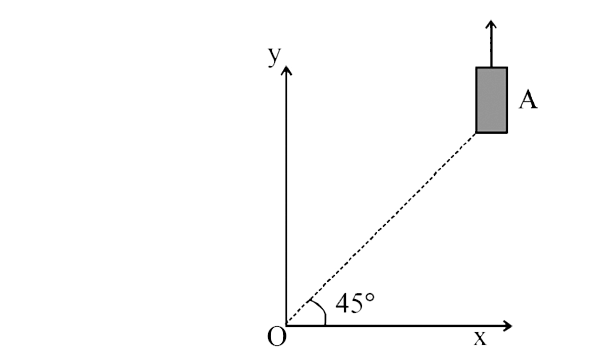 View Solution
View SolutionEvaluate ∫(sinx+cosx)dx√3+sin2x.
View SolutionThe value of I=∫π/20(sinx+cos)2√1+sin2xdx is
View SolutionEvaluate : ∫π/3π/6sinx+cosx√sin2x dx.
View SolutionEvaluate: ∫cosxsinx+√sinxdx
View Solution

