Is it true to say that area of segment of a circle is less than the area of its corresponding sector? Why ?
The correct Answer is:False
To determine whether the area of a segment of a circle is less than the area of its corresponding sector, we can analyze the two cases: the major segment and the minor segment.
1. Understanding the Definitions:
- A sector of a circle is a region enclosed by two radii and the arc between them.
- A segment of a circle is a region enclosed by a chord and the arc that subtends it.
2. Case 1: Major Segment:
- Consider a major segment formed by a chord AB and the arc ACB.
- The area of the major segment ACB includes the area of the triangle AOB (where O is the center of the circle).
- The area of the corresponding sector AOB is the area enclosed by the radii OA, OB, and the arc AB.
Comparison:
- The area of the major segment ACB is greater than the area of the sector AOB because the area of triangle AOB is included in the major segment.
3. Case 2: Minor Segment:
- Now consider a minor segment formed by the same chord AB and the arc ACB.
- The area of the minor segment ACB is less than the area of the corresponding sector AOB because the area of triangle AOB is included in the sector.
Comparison:
- The area of the sector AOB is greater than the area of the minor segment ACB.
4. Conclusion:
- The statement that the area of a segment of a circle is less than the area of its corresponding sector is true only for the minor segment.
- For the major segment, the area of the segment is greater than the area of the corresponding sector.
Final Statement:
Thus, it is not universally true that the area of a segment of a circle is less than the area of its corresponding sector; it depends on whether the segment is a minor or major segment.
- A sector of a circle is a region enclosed by two radii and the arc between them.
- A segment of a circle is a region enclosed by a chord and the arc that subtends it.
- Consider a major segment formed by a chord AB and the arc ACB.
- The area of the major segment ACB includes the area of the triangle AOB (where O is the center of the circle).
- The area of the corresponding sector AOB is the area enclosed by the radii OA, OB, and the arc AB.
- The area of the major segment ACB is greater than the area of the sector AOB because the area of triangle AOB is included in the major segment.
- Now consider a minor segment formed by the same chord AB and the arc ACB.
- The area of the minor segment ACB is less than the area of the corresponding sector AOB because the area of triangle AOB is included in the sector.
- The area of the sector AOB is greater than the area of the minor segment ACB.
- The statement that the area of a segment of a circle is less than the area of its corresponding sector is true only for the minor segment.
- For the major segment, the area of the segment is greater than the area of the corresponding sector.
Thus, it is not universally true that the area of a segment of a circle is less than the area of its corresponding sector; it depends on whether the segment is a minor or major segment.
Topper's Solved these Questions
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Short Answer Type Questions
16 Videos
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Long Answer Type Questions
20 Videos
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Long Answer Type Questions
20 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions
10 Videos
Similar Questions
Find the area of the minor segment of a circle of radius 14cm, when the angle of the corresponding sector is 60∘

View SolutionWhat is the area of the sector shown in
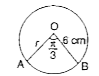
View SolutionFind the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60∘ . (use π=3.14)
View SolutionFind the area of the sector of a circle with radius 4 cm and of angle 30∘. Also, find the area of the corresponding major sector
View SolutionFind the area of the sector of a circle with radius 4 cm and of angle 30o . Also, find the area of the corresponding major sector. (Use π=3.14)
View SolutionFind the area of the sector of a circle with radius 4 cm and of angle 30o . Also, find the area of the corresponding major sector. (Use π=3.14)
View SolutionFind the area of the segment of a circle, given that the angle of the sector is 120o and the radius of the circle is 21 cm. (Take π=22/7)
View SolutionThe radius of a circle is 7 cm. Find its area
View SolutionFind the area of the shaded segment
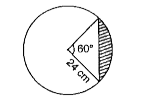
View SolutionFind the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
View Solution
