It takes 12000J of work to pull a sled 200m with a 120N force. Determine the angle of the rope with the horizontal.
To solve the problem, we need to determine the angle of the rope with the horizontal given the work done, the force applied, and the distance over which the sled is pulled.
1. Identify the given values:
- Work done (W) = 12000 J
- Force applied (F) = 120 N
- Distance (D) = 200 m
2. Recall the formula for work done:
The work done (W) when a force is applied at an angle to the direction of motion is given by:
W=F⋅D⋅cos(θ)
where θ is the angle between the force and the direction of motion.
3. Substitute the known values into the formula:
12000=120⋅200⋅cos(θ)
4. Calculate 120⋅200:
120⋅200=24000
So, we can rewrite the equation as:
12000=24000⋅cos(θ)
5. Isolate cos(θ):
To find cos(θ), divide both sides by 24000:
cos(θ)=1200024000=12
6. Find the angle θ:
We know that cos(60∘)=12, therefore:
θ=60∘
Final Answer:
The angle of the rope with the horizontal is 60∘.
---
- Work done (W) = 12000 J
- Force applied (F) = 120 N
- Distance (D) = 200 m
The work done (W) when a force is applied at an angle to the direction of motion is given by:
W=F⋅D⋅cos(θ)
where θ is the angle between the force and the direction of motion.
12000=120⋅200⋅cos(θ)
120⋅200=24000
So, we can rewrite the equation as:
12000=24000⋅cos(θ)
To find cos(θ), divide both sides by 24000:
cos(θ)=1200024000=12
We know that cos(60∘)=12, therefore:
θ=60∘
The angle of the rope with the horizontal is 60∘.
Topper's Solved these Questions
Similar Questions
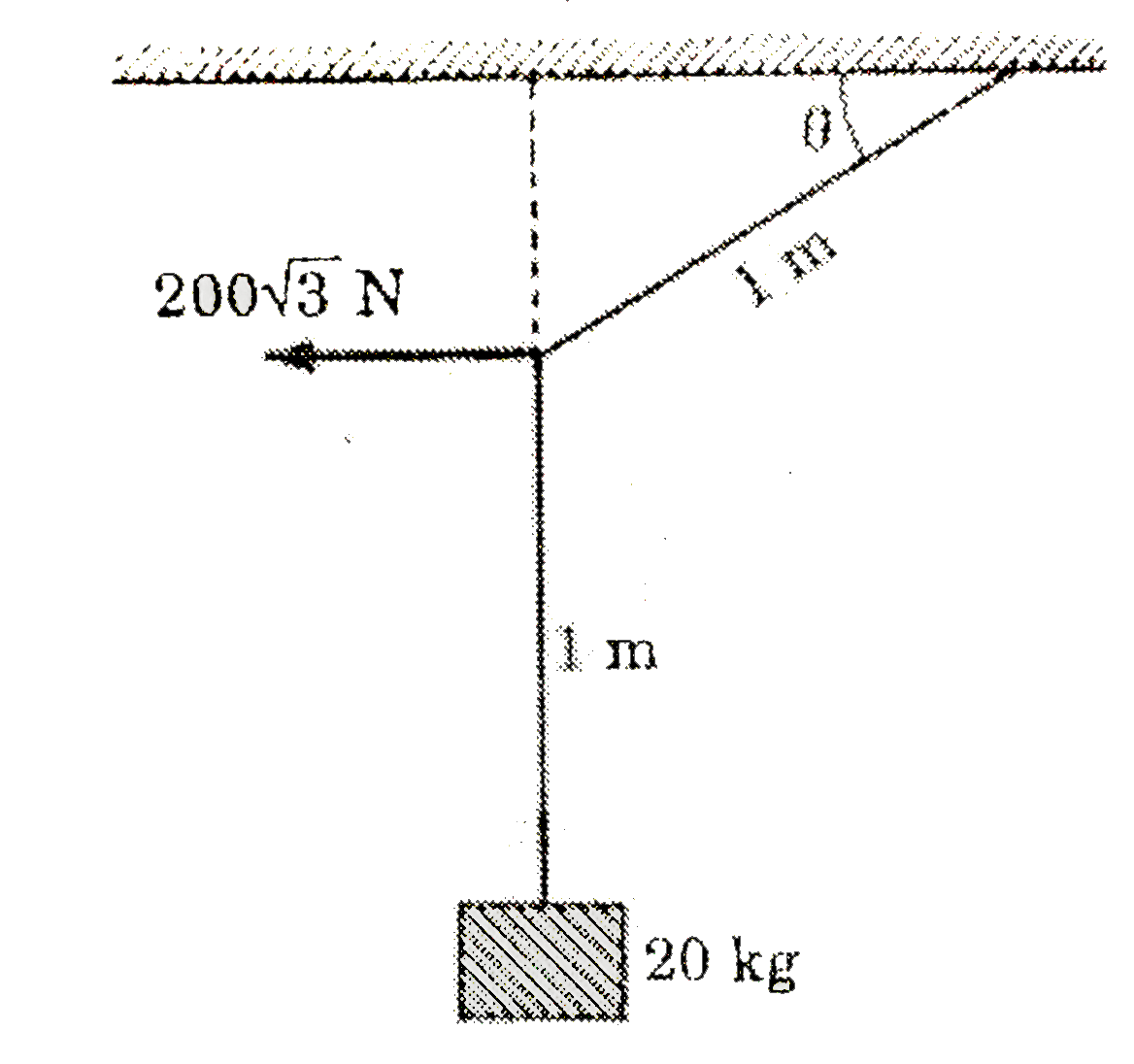
A mass of 20 kg is suspended by a rope of length 2 m from a ceiling. A force of 173.2 N in the horizontal direction is applied at the midpoint of the rope as shown in Fig. What is the angle the rope makes with the horizontal in equilibrium ? Take g = 10ms−2. Neglect mass of the rope.
View SolutionA rope of mass m is hung from a ceiling. The centre point is pulled down with a vertical force F. The tangent to the rope at its ends makes an angle α with horizontal ceiling. The two tangents at the lower point make an angle of θ with each other. Find θ .

View Solution
Knowledge Check
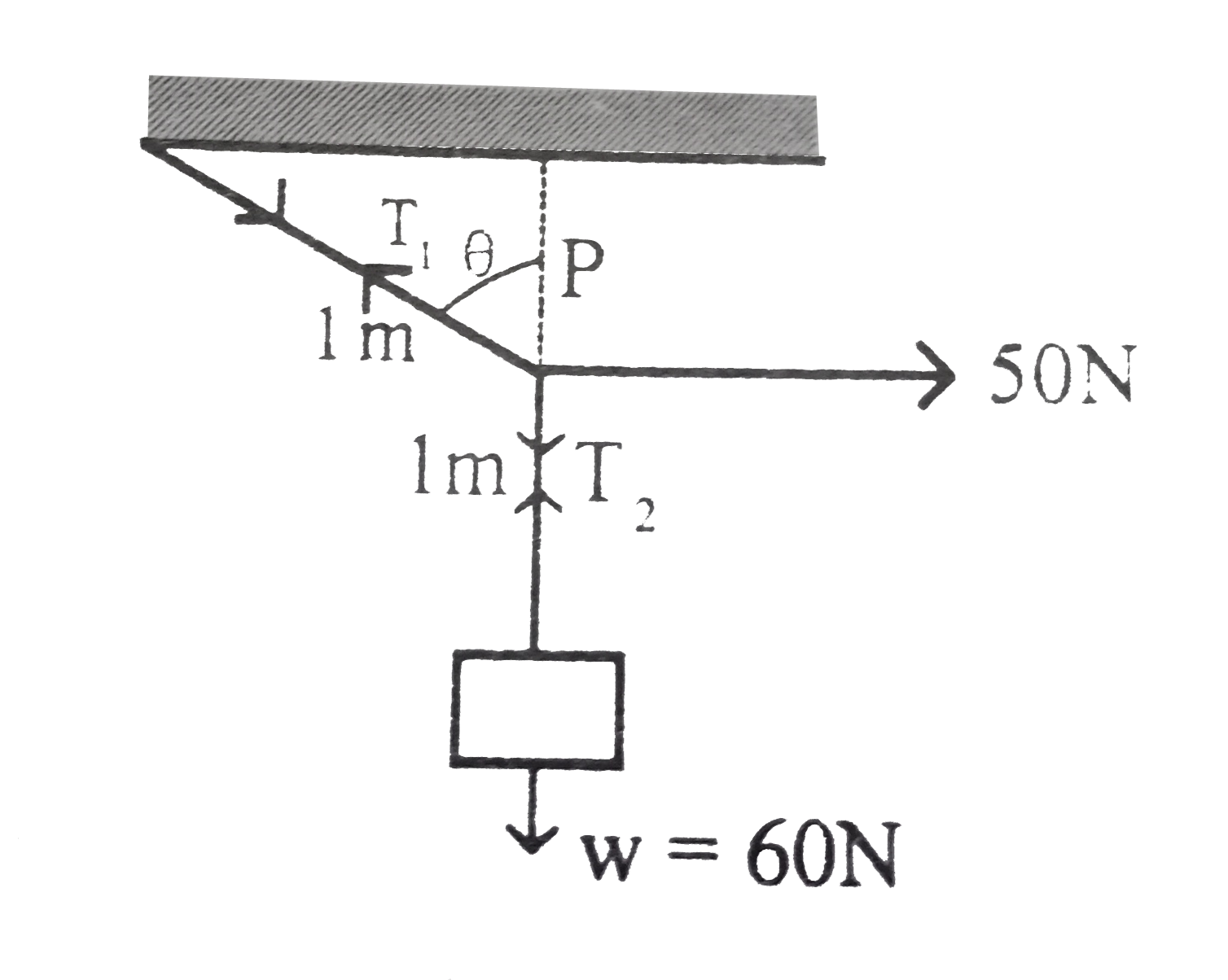
A mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
 Atan−1(45)Btan−1(54)Ctan−1(56)DNone of these
Atan−1(45)Btan−1(54)Ctan−1(56)DNone of theseThe work done in pulling up a block of wood weighing 200N for length of 10 m on a smooth plane inclined at an angle of 30∘ with the horizontal is
A18 KJB20 KJC10 KJDNoneA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
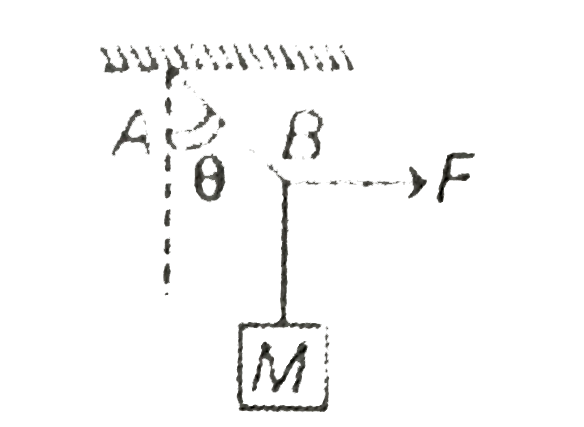 AF sinθBF/sinθCFcosθDF/cosθ
AF sinθBF/sinθCFcosθDF/cosθ
A mass of 10 kg is suspended vertically by a rope of length 2 m from a ceiling. A force of 60 N is applied at the middle point of the rope in the horizontal direction, as shown in Fig. Calculate the angle the rope makes with the vertical. Neglect the mass of the rope and take g=10ms−2.

View SolutionA boy pulls a sled of mass 5.0 kg with a rope that makes a 60.0∘ angle with respect to the horizontal surface of a frozen pond. The boy pulls on the rope with a force of 10.0 N, and the sled moves with constant velocity. What is the coefficient of friction between the sled and the ice?
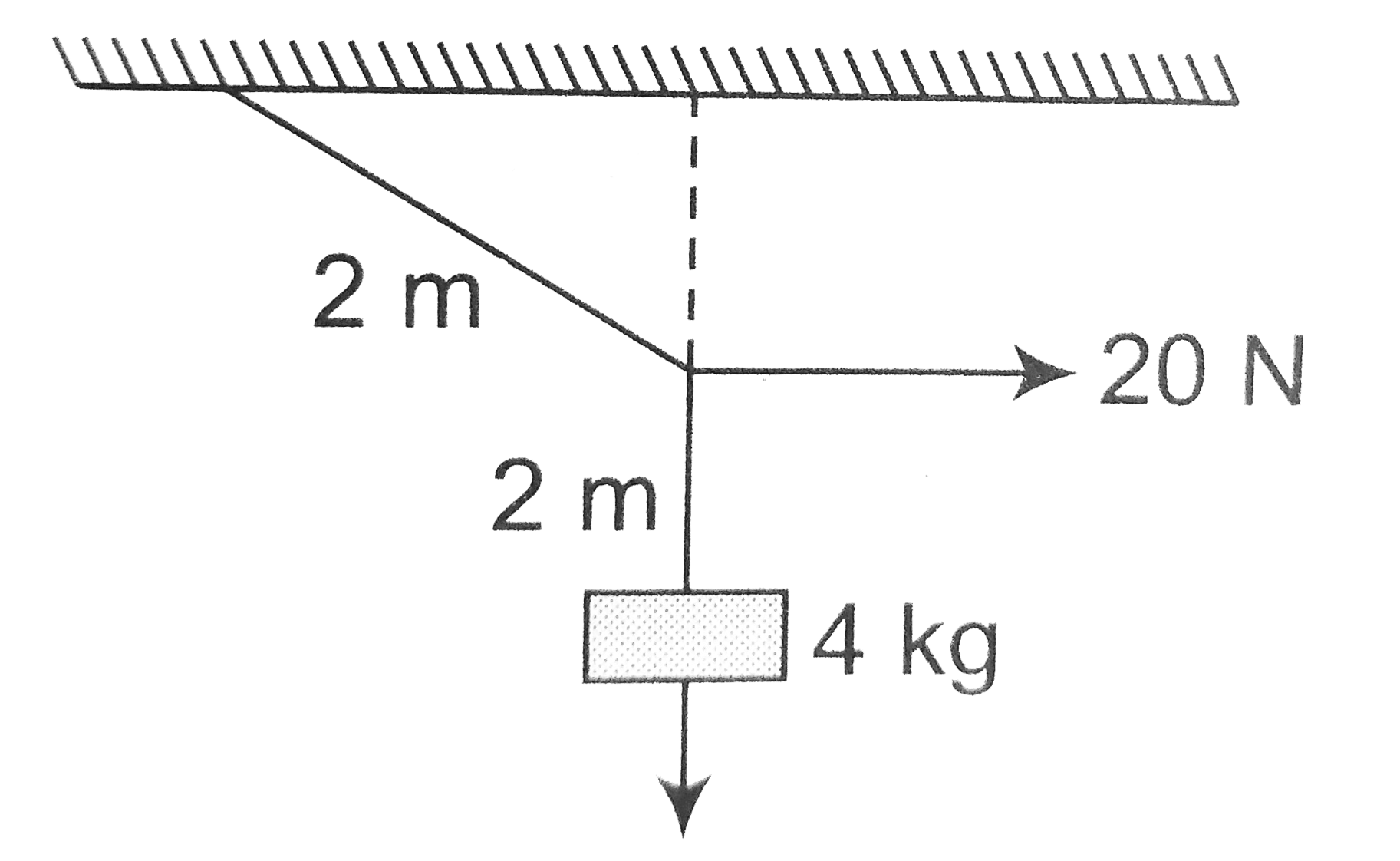
View SolutionA mass of 4kg is suspended by a rope of length 4m from a ceiling. A force of 20N in the horizontal direction is applied at the mid-point of the rope as shown in figure. What is the angle which the rope makes with the vertical in equilibrium? Neglect the mass of the rope. Take g=10ms−2 .
View SolutionA block of mass m is pulled along a horizontal surface by applying a force at an angle θ with the horizontal. If the block travels with a uniform velocity and has a displacement d and the coefficient of friction is μ, then the work done by the applied force is
View SolutionA mass of 20 kg is suspended by a rope of length 4 m from the ceiling. A force of 60 N is applied at the midpoint of the rope in the horizontal direction. What is the angle made by the rope with the vertical in equilibrium? Assume that the mass of the rope is negligible and g=10m/s2
View Solution
