KLMN is an isosceles trapezium whose diagonals cut at X and KL is parallel to NM. If ∠KNL=25∘,∠KMN=30∘∠KLN=40∘, find ∠NKX
The correct Answer is:85∘
To solve the problem step by step, we will use the properties of isosceles trapeziums and the relationships between angles formed by parallel lines and transversals.
Step 1: Understand the given information
We have an isosceles trapezium KLMN where KL is parallel to NM. The angles given are:
- ∠KNL=25∘
- ∠KMN=30∘
- ∠KLN=40∘
Step 2: Identify the angles at point X
Since KL is parallel to NM and KN is a transversal, we can use the property of alternate interior angles. Thus, we have:
- ∠KMN=∠NKX=30∘
Step 3: Calculate the exterior angle at point K
In triangle KNL, we can find the exterior angle at K, which is given by the sum of the two opposite interior angles:
- ∠KNL+∠KLN=25∘+40∘=65∘
- Therefore, the exterior angle ∠KMN (which is also ∠NKX) is:
- ∠NKX+∠KNL=70∘
Step 4: Set up the equation for triangle NKX
In triangle NKX, the sum of the angles is equal to 180∘:
- ∠NKX+∠KNL+∠KXN=180∘
- Substituting the known angles:
- ∠NKX+25∘+70∘=180∘
Step 5: Solve for angle NKX
Now, simplify the equation:
- ∠NKX+95∘=180∘
- Therefore, ∠NKX=180∘−95∘=85∘
Final Answer
Thus, the angle ∠NKX is 85∘.
---
We have an isosceles trapezium KLMN where KL is parallel to NM. The angles given are:
- ∠KNL=25∘
- ∠KMN=30∘
- ∠KLN=40∘
Since KL is parallel to NM and KN is a transversal, we can use the property of alternate interior angles. Thus, we have:
- ∠KMN=∠NKX=30∘
In triangle KNL, we can find the exterior angle at K, which is given by the sum of the two opposite interior angles:
- ∠KNL+∠KLN=25∘+40∘=65∘
- Therefore, the exterior angle ∠KMN (which is also ∠NKX) is:
- ∠NKX+∠KNL=70∘
In triangle NKX, the sum of the angles is equal to 180∘:
- ∠NKX+∠KNL+∠KXN=180∘
- Substituting the known angles:
- ∠NKX+25∘+70∘=180∘
Now, simplify the equation:
- ∠NKX+95∘=180∘
- Therefore, ∠NKX=180∘−95∘=85∘
Thus, the angle ∠NKX is 85∘.
Topper's Solved these Questions
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - QUESTION BANK - 23
20 Videos
- POLYGONS AND QUADRILATERALS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - SELF ASSESSMENT SHEET - 23
10 Videos
- PERCENTAGE AND ITS APPLICATIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )
10 Videos
- PROBABILITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -29
10 Videos
Similar Questions
Knowledge Check
In an isosceles trapezium ABCD, ∠C is equal to:
 A115∘B65∘C105∘D75∘
A115∘B65∘C105∘D75∘ABCD is a cyclic trapezium whose side AD and BC are parallel to each other. If ∠ABC=62∘ then the measure of the ∠BCD is :
A120∘B118∘C62∘D28∘ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=72∘, then the measure of the ∠BCD is
A162∘B18∘C108∘D72∘
In the figure, ∠CAE=30∘and∠AEB=120∘. Find ∠ADB
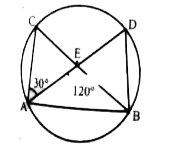
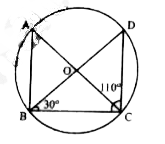
View SolutionIn this figure ∠DBC=30∘and∠BCD=110∘. Find ∠BAC
View Solution
In the figure above ∠QPS=2∠SPR,∠Q=∠R+40∘and∠PSR=120∘. Find ∠QPR
View Solution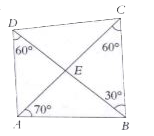
In the given figure ABCD is a quadrilateral ∠ADB=60∘,∠BAC=70∘,∠DBC=30∘,and∠ACB=60∘. Find ∠DAC
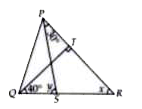
View SolutionIn figure, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find value of y-x
View Solution

