Let A = {1,2,3,4,5} Define on operation v by
a∨b=max{a,b}
Prepare its compostion table
Show that a is closed for the given operation and that the given operation is commutative
We prepare the table as given below
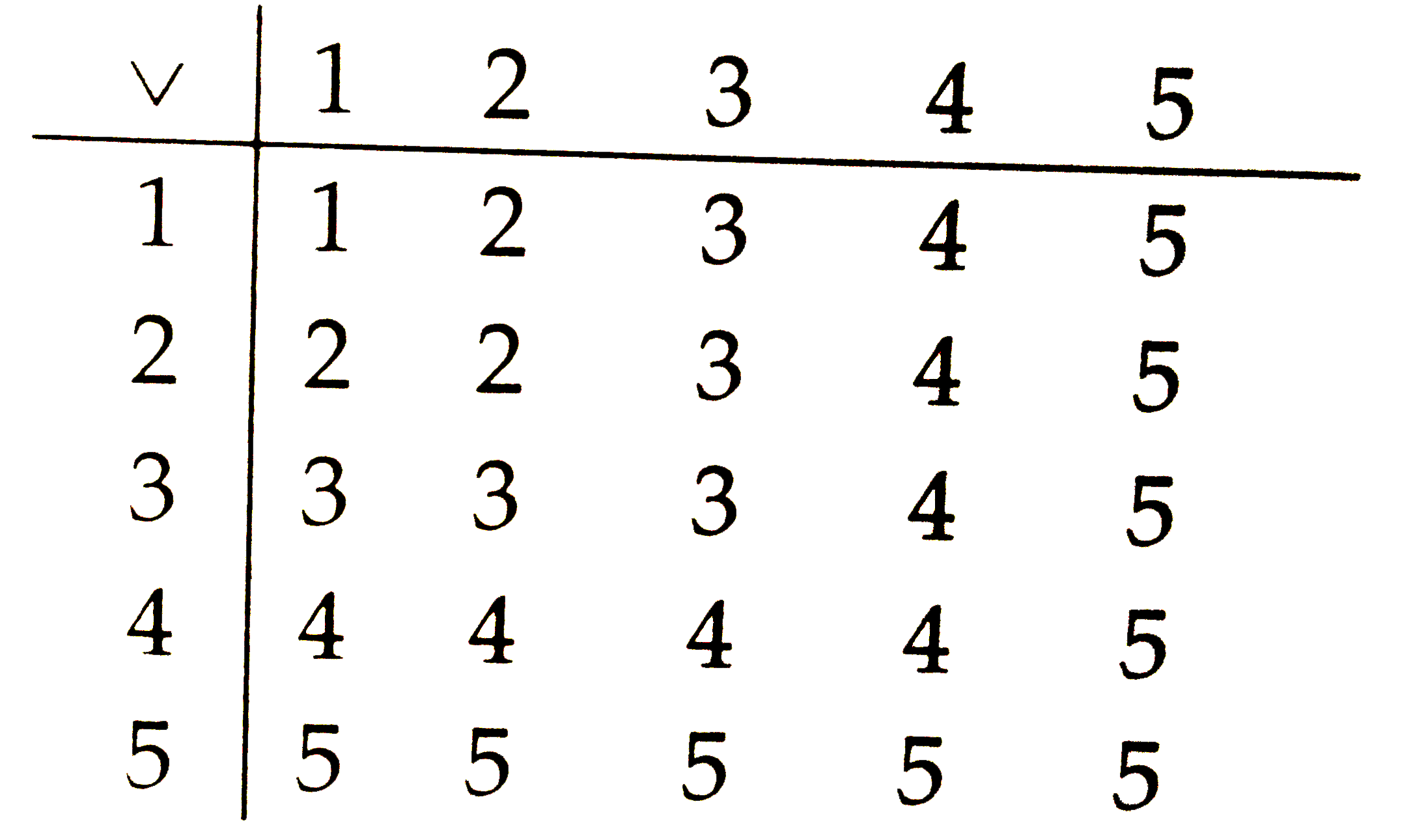
Closure property
since all the entries of the composition table are form the given set so closure property is satisfied
Commutative law
Clearly every row coincides with the corresponding column So commuative law is sastisfied
Topper's Solved these Questions
- BINARY OPERATIONSBOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3A
17 Videos
- BINARY OPERATIONSBOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3B
8 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - RS AGGARWALCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise 9C
9 Videos
Similar Questions
Let A= {1,2,3,4,5}. Define an operative V by a Vb= max. {a,b}. Prepare its composition table.
View SolutionShow that the binary operation * on Z defined by a⋅b=3a+7b is not commutative.
View SolutionShow that the binary operation '∗' defined from N×N→N and given by a∗b=2a+3b is not commutative.
View SolutionShow that the binary operation * on Z defined by a*b=3a+7b is not commutative.
View SolutionConsider the binary operation ∧ on the set {1,2,3,4,5} defined by a∧b=min{a,b}. Write the operation table of the operation.
View SolutionDefine * on Z by a*b =a-b+ab
show that * is a binary operation operation on z which is neither commutative nor associative
View SolutionExamine whether the binary operation ∗ defined on R by a∗b=ab+1 is commutative or not.
View SolutionConsider the binary operation ∗ on the set {1,2,3,4,5} defined by a∗b=min.{a,b}. Write the operation table of the operation ∗.
View SolutionConsider the binary operation ∗ on the set {1,2,3,4,5} defined by a∗b=min.{a,b}. Write the operation table of the operation ∗.
View SolutionConsider the binary operation ∧on the set {1,2,3,4,5}defined by a∧b= min {a,b}. Write the operation table of the operation ∧.
View Solution
