Let A=⎡⎢⎣abcpqrxyz⎤⎥⎦ and suppose then det (A) = 2, then det (B) equals, where B=⎡⎢⎣4x2a−p4y2b−q4z2c−r⎤⎥⎦
-2
-8
-16
8
The correct Answer is:C
To find the determinant of the matrix B given that the determinant of matrix A is 2, we will follow these steps:
Given:
A=⎡⎢⎣abcpqrxyz⎤⎥⎦
and
det(A)=2
We need to find:
B=⎡⎢⎣4x2a−p4y2b−q4z2c−r⎤⎥⎦
Step 1: Factor out constants from the determinant
Using the property of determinants that allows us to factor out constants from rows or columns, we can rewrite the determinant of B:
det(B)=det⎛⎜⎝⎡⎢⎣4x2a−p4y2b−q4z2c−r⎤⎥⎦⎞⎟⎠
We can factor out 4 from the first column, 2 from the second column, and −1 from the third column:
det(B)=4⋅2⋅(−1)⋅det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠
This simplifies to:
det(B)=−8⋅det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠
Step 2: Relate the determinant of B to A
Notice that the matrix inside the determinant is a rearrangement of the columns of A. Specifically, we can express it as:
det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠=det(A)
However, we will need to account for the column swaps.
Step 3: Interchange columns
1. Interchange column 1 and column 2:
det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠=−det⎛⎜⎝⎡⎢⎣axpbyqczr⎤⎥⎦⎞⎟⎠
2. Interchange column 2 and column 3:
det⎛⎜⎝⎡⎢⎣axpbyqczr⎤⎥⎦⎞⎟⎠=−det(A)
Step 4: Final expression for det(B)
Combining these results, we have:
det(B)=−8⋅(−det(A))=8⋅det(A)
Substituting det(A)=2:
det(B)=8⋅2=16
Step 5: Apply the negative sign from the earlier factorization
Thus, we have:
det(B)=−16
Conclusion
The final result is:
det(B)=−16
A=⎡⎢⎣abcpqrxyz⎤⎥⎦
and
det(A)=2
We need to find:
B=⎡⎢⎣4x2a−p4y2b−q4z2c−r⎤⎥⎦
Using the property of determinants that allows us to factor out constants from rows or columns, we can rewrite the determinant of B:
det(B)=det⎛⎜⎝⎡⎢⎣4x2a−p4y2b−q4z2c−r⎤⎥⎦⎞⎟⎠
We can factor out 4 from the first column, 2 from the second column, and −1 from the third column:
det(B)=4⋅2⋅(−1)⋅det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠
This simplifies to:
det(B)=−8⋅det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠
Notice that the matrix inside the determinant is a rearrangement of the columns of A. Specifically, we can express it as:
det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠=det(A)
However, we will need to account for the column swaps.
1. Interchange column 1 and column 2:
det⎛⎜⎝⎡⎢⎣xapybqzcr⎤⎥⎦⎞⎟⎠=−det⎛⎜⎝⎡⎢⎣axpbyqczr⎤⎥⎦⎞⎟⎠
2. Interchange column 2 and column 3:
det⎛⎜⎝⎡⎢⎣axpbyqczr⎤⎥⎦⎞⎟⎠=−det(A)
Combining these results, we have:
det(B)=−8⋅(−det(A))=8⋅det(A)
Substituting det(A)=2:
det(B)=8⋅2=16
Thus, we have:
det(B)=−16
The final result is:
det(B)=−16
Topper's Solved these Questions
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise (Passage Based Questions)
16 Videos
- MATRICES BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATRICES EXERCISE - Exercise For Session 4
9 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHS ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MONOTONICITY MAXIMA AND MINIMABOOK - ARIHANT MATHS ENGLISHCHAPTER - MONOTONICITY MAXIMA AND MINIMAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
29 Videos
Similar Questions
Let a determinant is given by A=∣∣ ∣ ∣∣abcpqrxyz∣∣ ∣ ∣∣ and suppose det.A=6. lf B=∣∣ ∣ ∣∣p+xq+yr+za+xb+yc+za+pb+qc+r∣∣ ∣ ∣∣ then
View SolutionIf ∣∣ ∣ ∣∣apxbqycrz∣∣ ∣ ∣∣=16, then the value of ∣∣ ∣ ∣∣p+xa+xa+pq+yb+yb+qr+zc+zc+r∣∣ ∣ ∣∣ is (a) 4 (b) 8 (c) 16 (d) 32
View SolutionProve that the value of each the following determinants is zero: ∣∣ ∣ ∣∣a−bb−cc−ax−yy−zz−xp−qq−rr−p∣∣ ∣ ∣∣
View SolutionLet A=[pqqp] such that det(A)=r where p,q,r all prime number, then trace of A is equal to
View SolutionIf ∣∣ ∣ ∣∣pq−yr−zp−xqr−zp−xq−yr∣∣ ∣ ∣∣=0 find the value of px+qy+rz
View SolutionThe value of ∣∣ ∣ ∣∣yzzxxyp2q3r111∣∣ ∣ ∣∣ , where x,y,z are respectively, pth, (2q)th, and (3r)th terms of an H.P. is a.−1 b. 0 c. 1 d. none of these
View SolutionIf A=⎡⎢⎣abcxyzpqr⎤⎥⎦,B=⎡⎢⎣q−by−pa−xr−cz⎤⎥⎦ and if A is
invertible, then which of the following is not true?
View SolutionIf A=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣andB=∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣, then
View SolutionProve that: ∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣=∣∣ ∣ ∣∣ybqxapzcr∣∣ ∣ ∣∣
View SolutionMatch the columns and choose correct options.
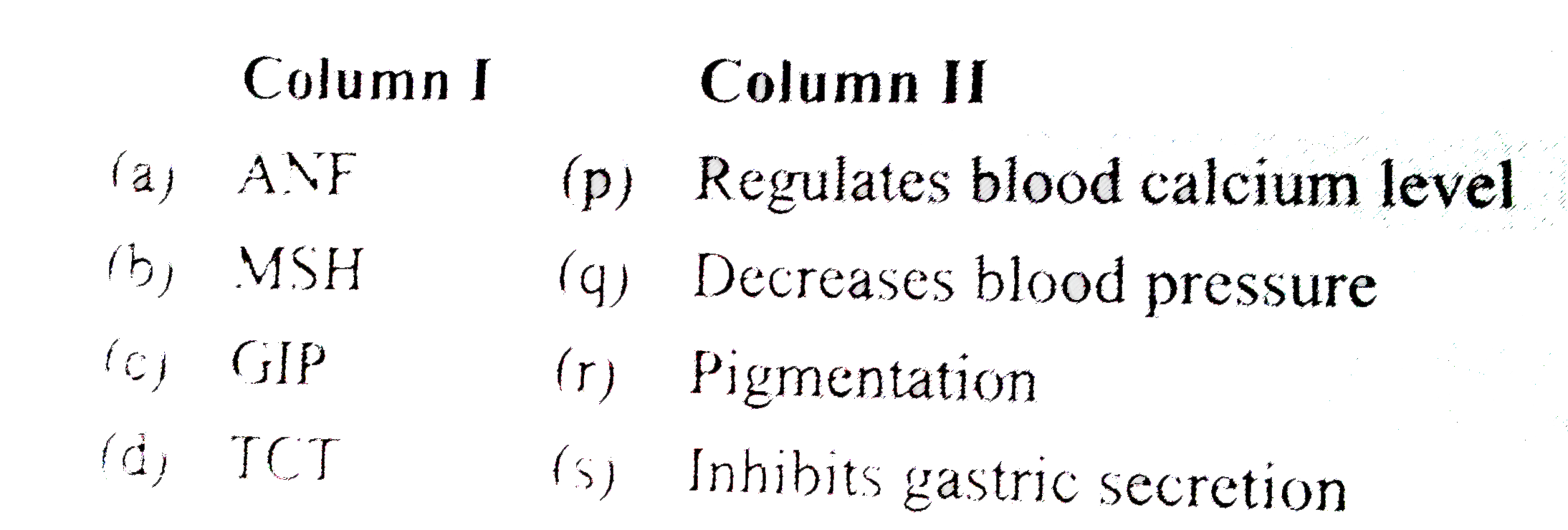
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-q
View Solution
