Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0
Video Solution
Text Solution
Let f(x)=x2+bax+ca .
Accounting to the questions, we have the following graph.
From the graph.
f(−1)<0andf(1)<0
⇒1+ca−ba<0and1+ca+ba<0
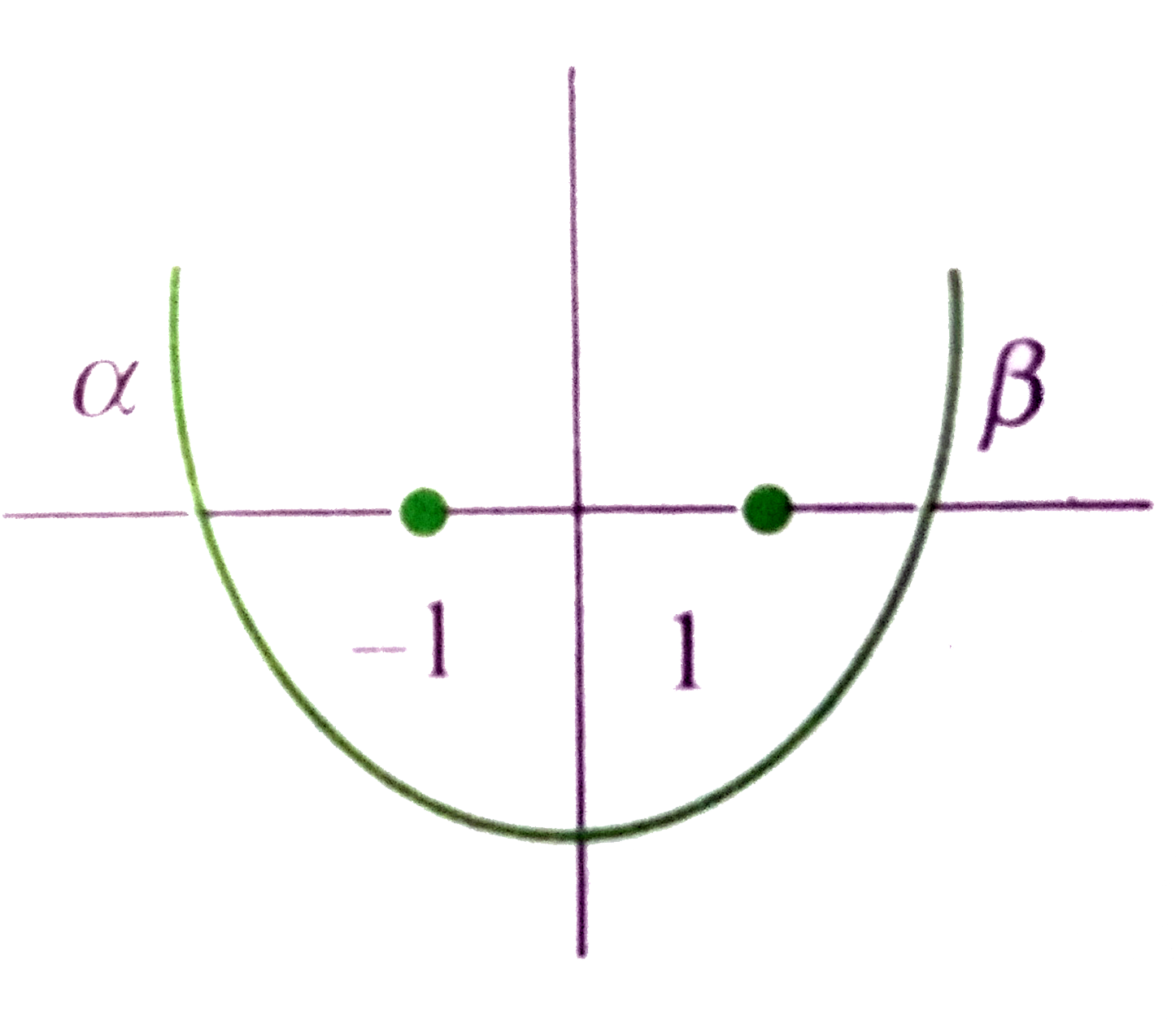
⇒1+ca+∣∣∣ba∣∣∣<0 .
|
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.13
9 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single)
89 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.11
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Let a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
Aless than zeroBgreater than zeroCequal to zeroDequal to b2−4acLet a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
Aless than zeroBgreater than zeroCequal to zeroDequal to b2−4acLet a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
Aa. less than -1Bb. greater than zeroCc. equal to zeroDd. equal to b2−4ac
If the equation ax2+bx+c=0(a>0) has two real roots αandβ such that α<−2 and β>2, then which of the following statements is/are true? (a)a−|b|+c<0 (b)c<0,b2−4ac>0 (c) 4a−2|b|+c<0 (d) 9a−3|b|+c<0
View SolutionIf ax2+(b−c)x+a−b−c=0 has unequal real roots for all c∈R,then
View SolutionIf a,b,c∈R and the quadratic equation x2+(a+b)x+c=0 has no real roots then
View SolutionIf b2<2ac , then prove that ax3+bx2+cx+d=0 has exactly one real root.
View SolutionIf ax2+bx+c=0 has no real roots and a, b, c ∈ R such that a+c>0, then
View Solution
