Let A be a set containing elements. A subset P of the set A is chosen at random. The set A is reconstructed by replacing the elements of P, and another subset Q of A is chosen at random. The probability that P∩Q contains exactly m(m<n) elements, is
3n−m4n
.nCm.3m4n
.nCm.3n−m4n
none of these
The correct Answer is:C
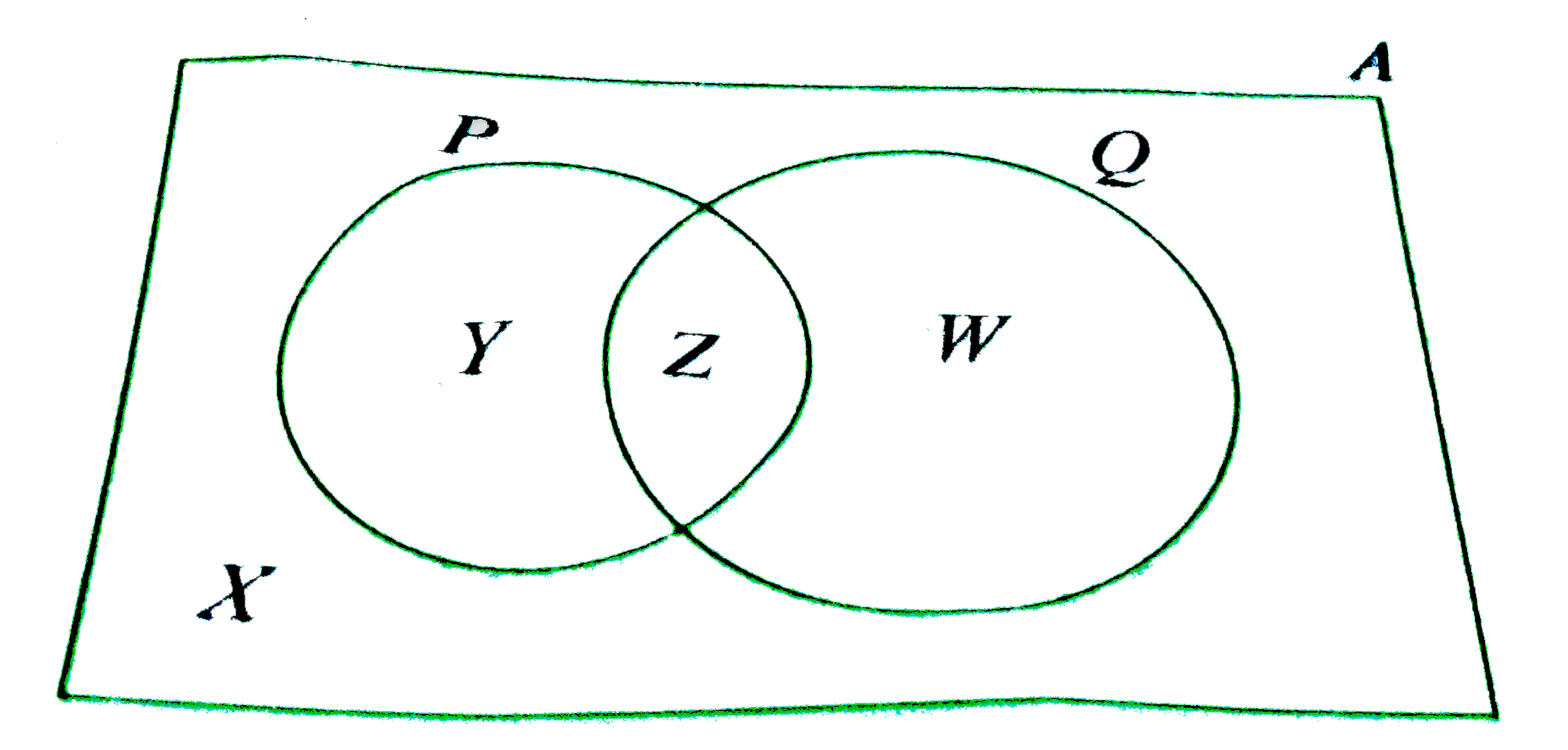
Sets P and Q are subsets of set A. Sets P and Q are dividing set A in four regions X, Y, Z and W.
∴ Total number of cases
= Number of ways in which n elements can be distributed in four regions = 4n
If set (P∩Q) has exactly m elements, we can select these m elements in .nCm ways. Remaining n - m elements can be distributed in the regions X, Y and W in 3n−m ways.
∴ Number of favourable ways = .nCm×3n−m
∴ Required probability = .nCm×3n−m4n
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Multiple)
8 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Comprehension)
14 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.3
7 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
Similar Questions
A subset A of the set X={1.2,3.....100} is chosen at random. The set X is reconstructed by replacing the elements of A, and another subset B of X is chosen at random. Then the probability that A∩B contains exactly 10 elements is
View SolutionA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The Probability that P∪Q contain just one element, is
View Solution
Knowledge Check
A subset A of the set X={1,2,3,..,100} is chosen at random. The set X is reconstructed by replacing the elements of A, and another subset B of X is chosen at random. The probability that A∩B contains exactly 10 elements, is
A.100C10(34)90B.100C10(12)100C.100C10×3904100Dnone of theseA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The probability that P =Q, is
A12nB(34)nC(14)nD(23)nA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The Probability that P∩Q contain just one element, is
A(34)nBn(34)nCn3(34)nDn4(34)n
A is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The Probability that P∪Q=A, is
View SolutionA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The Probability that Q is a subset of P, is
View SolutionA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The probability that P and Q are disjoint sets, is
View SolutionA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The probability that Q contains just one element more than P, is
View SolutionA is a set containing n elements. A subset P of A is chosen at random. The set A is reconstructed by replacing the elements of P. A subset Q is again chosen at random. The Probability that P and Q have equal number of elements, is
View Solution
