Let A be an inbertible matrix. Which of the following is not true?
(AT)−1=(A−1)T
A−1=|A|−1
(A2)−1=(A−1)2
∣∣A−1∣∣=|A|−1
The correct Answer is:B
To determine which statement is not true regarding the invertible matrix A, we will analyze each option step by step.
1. Understanding Invertible Matrices:
An invertible matrix A is one that has an inverse denoted by A−1 such that:
A⋅A−1=I
where I is the identity matrix.
2. Option A: (AT)−1=(A−1)T
- This is a known property of matrices. The inverse of the transpose of a matrix is equal to the transpose of the inverse of that matrix. Thus, this statement is true.
3. Option B: A−1=det(A−1)
- Here, A−1 is a matrix, while det(A−1) is a scalar (a number). A matrix cannot equal a scalar. Therefore, this statement is not true.
4. Option C: A−2=(A2)−1
- To check this, we can multiply both sides by A2:
A−2⋅A2=Iand(A2)−1⋅A2=I
- Both sides yield the identity matrix, confirming that this statement is true.
5. Option D: det(A−1)=1det(A)
- This is another known property of determinants. The determinant of the inverse of a matrix is equal to the reciprocal of the determinant of the matrix. Thus, this statement is true.
Conclusion:
The only statement that is not true is Option B: A−1=det(A−1).
---
An invertible matrix A is one that has an inverse denoted by A−1 such that:
A⋅A−1=I
where I is the identity matrix.
- This is a known property of matrices. The inverse of the transpose of a matrix is equal to the transpose of the inverse of that matrix. Thus, this statement is true.
- Here, A−1 is a matrix, while det(A−1) is a scalar (a number). A matrix cannot equal a scalar. Therefore, this statement is not true.
- To check this, we can multiply both sides by A2:
A−2⋅A2=Iand(A2)−1⋅A2=I
- Both sides yield the identity matrix, confirming that this statement is true.
- This is another known property of determinants. The determinant of the inverse of a matrix is equal to the reciprocal of the determinant of the matrix. Thus, this statement is true.
The only statement that is not true is Option B: A−1=det(A−1).
Topper's Solved these Questions
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Section I - Assertion Reason Type
12 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Exercise
79 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Chapter Test
30 Videos
- LOGARITHMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LOGARITHMSEXERCISE - Chapter Test
21 Videos
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise
28 Videos
Similar Questions
Knowledge Check
Which of the following statement is not true?
AAll identity matrices are square matrixBAll null matrices are square matrixCFor a square matrix number of rows is equal to the number of columnsDA square matrix all of whose elements except those in the leading diagonal are zero is the diagonal matrixWhich of the following statement is not true?
AAll identity matrices are square matrixBAll null matrices are square matrixCFor a square matrix number of rows is equal to the number of columnsDA square matrix all of whose elements except those in the leading diagonal are zero is the diagonal matrix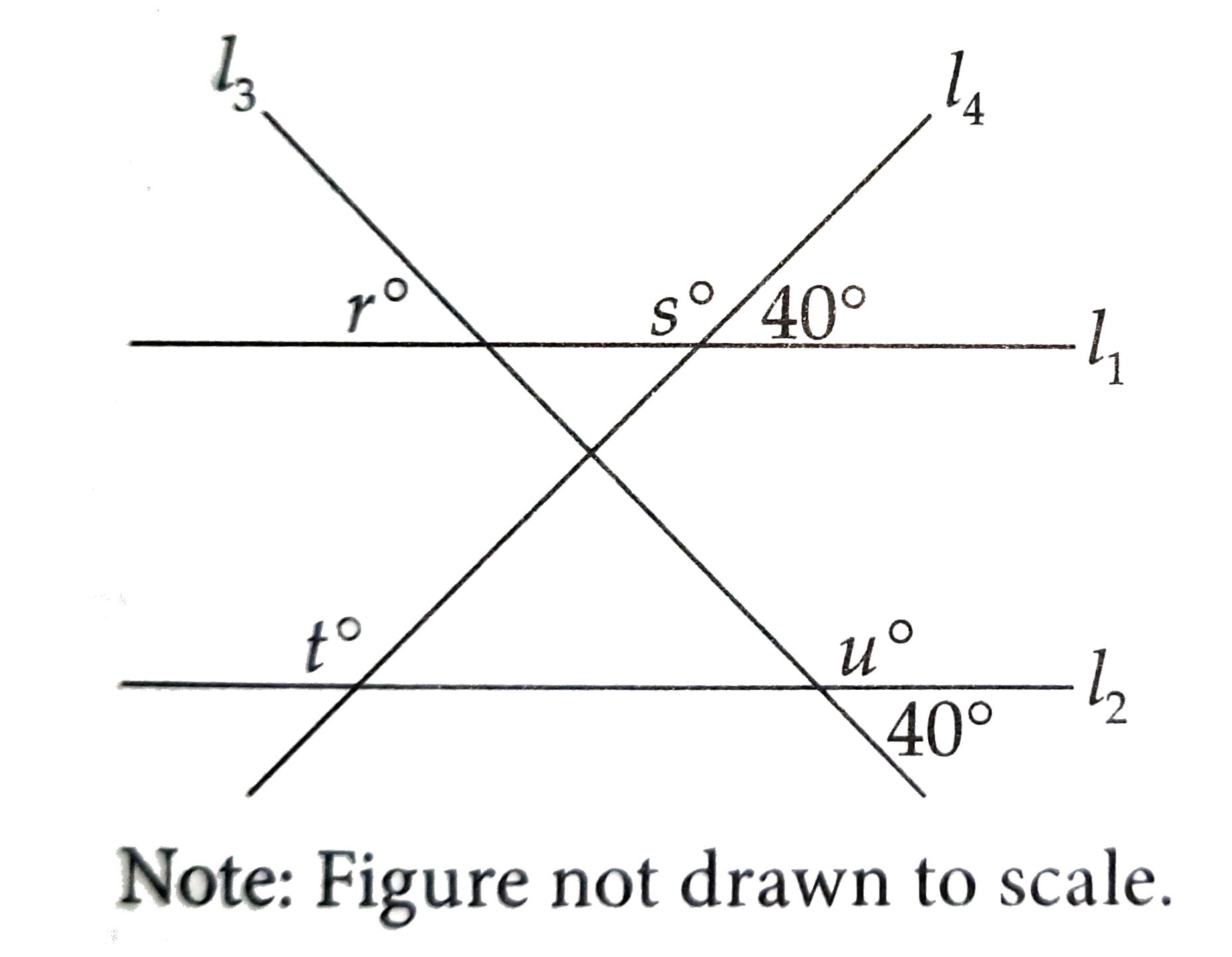
Which of the following must be true?Al1∣∣l2Bl3 bisects l4Cs=tDu=140∘
If A is an invertible matrix, then which of the following is not true (A2)−1=(A−1)2 (b) ∣∣A−1∣∣=|A|−1 (c) (AT)−1=(A−1)T (d) |A|≠0
View Solutionwhich of the following statements is not true ?
View SolutionWhich of the following is not true for a bike?
View SolutionWhich of the following statements is not true
View SolutionWhich of the following is a row matrix ?
View Solution
